RSA算法原理——（3）RSA加解密過程及公式論證

上期（RSA簡介及基礎數論知識）爲大家介紹了：互質、歐拉函數、歐拉定理、模反元素 這四個數論的知識點，而這四個知識點是理解RSA加密算法的基石，忘了的同學可以快速的回顧一遍。

一、目前常見加密算法簡介
二、RSA算法介紹及數論知識介紹
三、RSA加解密過程及公式論證

三、RSA加解密過程及公式論證

今天的內容主要分爲三個部分：

• rsa密鑰生成過程： 講解如何生成公鑰和私鑰
• rsa加解密演示： 演示加密解密的過程
• rsa公式論證：解密公式的證明

1、rsa密鑰生成過程

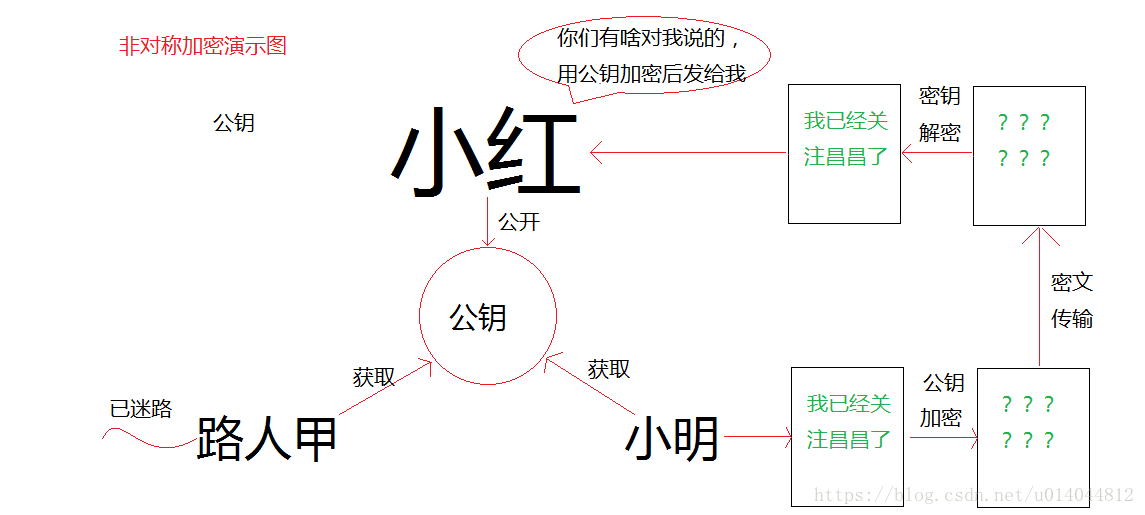
大家都知道rsa加密算法是一種非對稱加密算法，也就意味着加密和解密是使用不同的密鑰，而這不同的密鑰是如何生成的呢？下面我們來模擬下小紅是如何生成公鑰和私鑰的。

六步生成密鑰：

（1）隨機選擇兩個不相等的質數p和q

小紅隨機選擇選擇了61和53。（實際應用中，這兩個質數越大，就越難破解）

（2）計算p和q的乘積n

n = 61×53 = 3233

n的長度就是密鑰長度，3233寫成二進制是110010100001，一共有12位，所以這個密鑰就是12位。實際應用中，RSA密鑰一般是1024位，重要場合則爲2048位。

（3）計算n的歐拉函數φ(n)

這裏利用我們上篇講到的歐拉函數求解的第四種情況：

如果n可以分解成兩個互質的整數之積，即：n = p1 × p2，則φ(n) = φ(p1p2) = φ(p1)φ(p2)，所以φ(3233) = φ(61x53) = φ(61)φ(53)

又因爲61和53都是質數，所以可以根據歐拉函數求解的第二種情況：

如果n是質數，則 φ(n)=n-1，所以φ(3233) = φ(61x53) = φ(61)φ(53)=60x52=3120

所以 φ(n)=3120

（4）隨機選擇一個整數e，條件是1< e < φ(n)，且e與φ(n) 互質

小紅就在1到3120之間，隨機選擇了17。（實際應用中，常常選擇65537）

（5）計算e對於φ(n)的模反元素d

讓我們來回顧一下什麼是模反元素：
所謂“模反元素”就是指有一個整數d，可以使得ed除以φ(n)的餘數爲1，公式表示：

ed≡1(modφ(n))$$ed\equiv 1(mod\phi (n))$$

這個公式等價於

ed–kφ(n)=1$$ed–k\phi (n)=1$$

將e=17、φ(n)=3120代入得：

17d–3120k=1$$17d–3120k=1$$

設x=d、y=-k，得

17x+3120y=1$$17x+3120y=1$$

所以我們要求的模反元素d就是對上面的二元一次方程求解

根據擴展歐幾里得算法（輾轉相除法）求解：

上圖我們使用擴展歐幾里得求得x=-367，所以d=x=-367，但通常我們習慣取正整數，這樣方便計算，還記得我們上節講過的模反元素的特性嗎：

3和11互質，那麼3的模反元素就是4，因爲 (3 × 4)-1 可以被11整除。顯然，模反元素不止一個， 4加減11的整數倍都是3的模反元素 {…,-18,-7,4,15,26,…}，即如果b是a的模反元素，則 b+kn 都是a的模反元素。

所以我們取d=d+kφ(n)=-367+1x3120=2753，到這裏所有的計算已經全部完畢！

（6）將n和e封裝成公鑰，n和d封裝成私鑰

讓我們來回顧一下我們一共出現的6個數字：

1. p=61; 隨機數與q互質
2. q=53;隨機數與p互質
3. n=p*q=61*53=3233
4. φ(n)=φ(p*q)=φ(61x53) = φ(61)φ(53)=60x52=3120
5. e=17; 隨機數，條件是1< e < φ(n)，且e與φ(n) 互質
6. d=2753; e對於φ(n)的模反元素d

在這個例子中n=3233，e=17，d=2753，所以公鑰就是 (n,e)=(3233,17)，私鑰就是(n,d)=(3233, 2753)，這樣小紅就將公鑰公佈出去，自己保存好私鑰就可以啦！

至此我們公鑰、私鑰就生成完畢，是不是覺得並不是很難呢？是不是有點懷疑私鑰會不會被人破解呢？下面我們來看看如何才能暴力破解私鑰。

（7）rsa算法可靠性

回顧我們一共生成了六個數字：p q n φ(n) e d，這六個數字之中，公鑰用到了兩個（n和e），其餘四個數字都是不公開的。其中最關鍵的是d，因爲n和d組成了私鑰，一旦d泄漏，就等於私鑰泄漏。

那麼，有無可能在已知n和e的情況下，推導出d？

1. ed≡1 (mod φ(n))。只有知道e和φ(n)，才能算出d
2. φ(n)=(p-1)(q-1)。只有知道p和q，才能算出φ(n)
3. n=pq。只有將n因數分解，才能算出p和q

結論：如果n可以被因數分解，d就可以算出，也就意味着私鑰被破解。

看到這裏有同學可能會驚呼：原來破解RSA算法的方法這個簡單？？？

可是，大整數的因數分解，是一件非常困難的事情。也許你可以對3233進行因數分解（61×53），但是你沒辦法對下面的大整數分解：

123018668453011775513049495838496272077285356959533479219732245215172640050726
365751874520219978646938995647494277406384592519255732630345373154826850791702
6122142913461670429214311602221240479274737794080665351419597459856902143413

它等於兩個質素的乘積：

33478071698956898786044169
84821269081770479498371376
85689124313889828837938780
02287614711652531743087737
814467999489
×
36746043666799590428244633
79962795263227915816434308
76426760322838157396665112
79233373417143396810270092
798736308917

這也是目前維基百科記錄的人類分解的最大整數（232個十進制位，768個二進制位），除了暴力破解，還沒有發現別的有效方法。所以限制人類分解大整數的是計算機的計算能力，相信如果有一天真正的量子計算機問世後，又會引發一輪安全加密競賽！

• 1999年，RSA-155 (512 bits)被成功分解，花了五個月時間（約8000 MIPS年）和224 CPU hours在一臺有3.2G中央內存的Cray C916計算機上完成。
• 2009年12月12日，編號爲RSA-768（768 bits, 232 digits）數也被成功分解[10]。這一事件威脅了現通行的1024-bit密鑰的安全性，普遍認爲用戶應儘快升級到2048-bit或以上。

2、rsa加解密演示

小紅有了公鑰和私鑰這樣就可以進行加解密了，於是小紅拉着小明一起來測試一下！

（1）加密要用公鑰 (n,e)

假設小明先測試性的給小紅髮一個字母m=“A”，我們都知道在通信傳輸中只能傳輸0和1，所以我們先將“A”轉ascii碼爲65，所以m=65，m必須是整數（字符串可以取ascii值或unicode值），且m必須小於n。

所謂”加密”，就是使用下面的加密公式算出下式的密文c：

me≡c(modn)$$m^e\equiv c(modn)$$

小明得到的公鑰是(n,e)=(3233, 17)，m=65，那麼得到下面的等式：

6517≡c(mod3233)$${65}^{17}\equiv c(mod3233)$$

小明通過計算器一算c=2790，所以他就把2790發給小紅了。

（2）解密要用私鑰(n,d)

小紅拿到小明發過來的密文c=2790，就用下面的公式進行解密出明文m：

cd≡m(modn)$$c^d\equiv m(modn)$$

而小紅的私鑰爲：(n,d) = (3233,2753)，所以得到下面的等式：

27902753≡m(mod3233)$${2790}^{2753}\equiv m(mod3233)$$

小紅通過計算器一算，得m=65，然後小紅對照着ascii碼錶得出65對應得字母爲A。

至此，整個加解密過程就演示完了，我們來總結一下：

1. 小明獲取到小紅的公鑰(n,e)=(3233,17)
2. 小明選取發送的消息m=A=65，注意m要小於n，如果消息大於n，則可以分段加密！
3. 小明通過加密公式：m^e ≡ c (mod n) 算出密文c=2790
4. 小紅獲取到小明的密文c=2790
5. 小紅使用解密公式：c^d ≡ m (mod n) 算法明文m=65=A

我們可以看到，其實RSA加密算法最核心的就是用公式來加解密，那麼我們會有個疑問？爲什麼解密公式一定可以得到明文m呢？也就是說這個公式是怎麼推導出來的？公式一定成立嗎？

感興趣的同學我們可以來一起證明一下解密公式，這也是整個RSA加密算法的最後最核心的一個知識點了。這裏我會一步一步的推理，儘可能通俗易懂；

3、rsa公式論證

首先讓我們再來回顧一下我們一共出現的8個數字

1. p： 隨機數與q互質
2. q：隨機數與p互質
3. n=p*q
4. φ(n)=φ(p*q)=φ(p)*φ(q)=(p-1)(q-1)
5. e： 隨機數，條件是1< e < φ(n)，且e與φ(n) 互質
6. d：e對於φ(n)的模反元素d：ed≡1 (mod φ(n))
7. m：小明發送的明文
8. c：小明用公鑰加密後的密文

驗證rsa算法成立，主要就是驗證解密公式成立：

解密公式：cd≡m(modn)$$解密公式：c^d\equiv m(modn)$$

根據加密公式：

加密公式：me≡c(modn)→c=me–kn$$加密公式：m^e\equiv c(modn)\to c=m^e–kn$$

將c代入要我們要證明的那個解密公式：

(me–kn)d≡m(modn)$$(m^e–kn{)}^d\equiv m(modn)$$

上式等同於下面的公式，原因如下

med≡m(modn)$$m^{ed}\equiv m(modn)$$

原因：我們都知道下面的二元一次方程分解，只有第一項不包含n，而所有包含n的項在對n 取餘 的操作中都可以消掉。因此得出了上面那個結論

(2–2n)2=4−8n+4n2$$(2–2n{)}^2=4-8n+4n^2$$

又因爲生成密鑰的第五步中我們取e並求了他對φ(n)的模反元素d：

ed≡1(modφ(n))→ed=hφ(n)+1$$ed\equiv 1(mod\phi (n))\to ed=h\phi (n)+1$$

所以將ed代入上式得

mhφ(n)+1≡m(modn)$$m^{h\phi (n)+1}\equiv m(modn)$$

所以，我們只要證明這個公式成立，就證明解密公式的成立，也就證明了RSA算法的成立。

下面我們分兩種情況來驗證上面的例子

（1） m與n互質

根據歐拉定理：如果兩個正整數a和n互質，則n的歐拉函數 φ(n) 可以讓下面的等式成立：

aφ(n)≡1(modn)$$a^{\phi (n)}\equiv 1(modn)$$

證明：因爲m與n互質，得

mφ(n)≡1(modn)→mφ(n)=1+kn→(mφ(n))h=(1+kn)h$$m^{\phi (n)}\equiv 1(modn)\to m^{\phi (n)}=1+kn\to (m^{\phi (n)}{)}^h=(1+kn{)}^h$$

而(1 + kn)^h對n取模爲1，因爲對(1 + kn)^h拆分只有第一項1不含有n，所以有

(mφ(n))h=(1+kn)h≡1(modn)$$(m^{\phi (n)}{)}^h=(1+kn{)}^h\equiv 1(modn)$$

同理

(mφ(n))h≡1(modn)→(mφ(n))h=1+kn→(mφ(n))h∗m=(1+kn)∗m$$(m^{\phi (n)}{)}^h\equiv 1(modn)\to (m^{\phi (n)}{)}^h=1+kn\to (m^{\phi (n)}{)}^h\ast m=(1+kn)\ast m$$

而 (1 + kn)*m對n取模爲m，因爲前面說過0 < m < n，所以有

(mφ(n))h∗m=(1+kn)∗m≡m(modn)→mhφ(n)+1≡m(modn)$$(m^{\phi (n)}{)}^h\ast m=(1+kn)\ast m\equiv m(modn)\to m^{h\phi (n)+1}\equiv m(modn)$$

當m與n互質時，證明原式成功！！！

（2） m與n不是互質關係

此時m與n不互質，所以m與n必定有除1以外的公因子，而又因爲n等於質數p和質數q的乘積，所以m必然等於kp或kq。

以 m = kp爲例，考慮到這時m與質數q必然互質，則根據歐拉定理和歐拉函數（第二種：當q爲質數，則φ(q)=q-1）使下面的式子成立：

(kp)φ(q)≡1(modq)→(kp)q−1≡1(modq)$$(kp{)}^{\phi (q)}\equiv 1(modq)\to (kp{)}^{q-1}\equiv 1(modq)$$

同上（m與n互質中）證明原理可得：

[(kp)q−1]h(p−1)×kp≡kp(modq)→(kp)h(p−1)(q−1)+1≡kp(modq)$$[(kp{)}^{q-1}{]}^{h(p-1)}\times kp\equiv kp(modq)\to (kp{)}^{h(p-1)(q-1)+1}\equiv kp(modq)$$

又因爲

ed≡1(modφ(n))→ed=hφ(n)+1→ed=h(p−1)(q−1)+1$$ed\equiv 1(mod\phi (n))\to ed=h\phi (n)+1\to ed=h(p-1)(q-1)+1$$

將ed代入上式

(kp)ed≡kp(modq)→(kp)ed=tq+kp$$(kp{)}^{ed}\equiv kp(modq)\to (kp{)}^{ed}=tq+kp$$

上式中，等式左邊(kp)^ed對p取模爲0，右邊kp對p取模也爲0，所以tq一定能整除p，但q是與p互質的，所以t必然能整除p，設t=rp，得

(kp)ed=rpq+kp$$(kp{)}^{ed}=rpq+kp$$

因爲 m=kp，n=pq，所以

med=rn+m→med≡m(modn)$$m^{ed}=rn+m\to m^{ed}\equiv m(modn)$$

又因爲生成密鑰的第五步中我們取e並求了他對φ(n)的模反元素d：

ed≡1(modφ(n))→ed=hφ(n)+1$$ed\equiv 1(mod\phi (n))\to ed=h\phi (n)+1$$

將ed代入上式得：

mhφ(n)+1≡m(modn)$$m^{h\phi (n)+1}\equiv m(modn)$$

當m與n不互質時，證明原式成功！！！

附手稿：

關注昌昌不迷路~