斐波那契序列的遞歸和非遞歸的實現

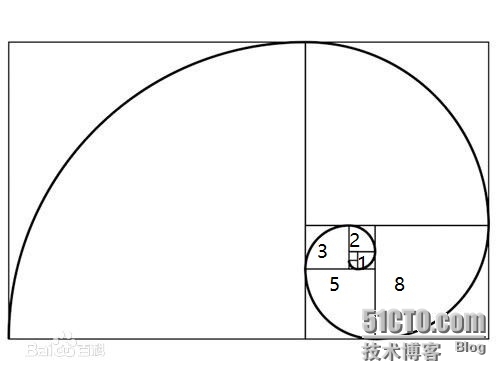
  斐波那契數列（Fibonacci sequence），又稱黃金分割數列、因數學家列昂納多·斐波那契（Leonardoda Fibonacci[1]）以兔子繁殖爲例子而引入，故又稱爲“兔子數列”。
  指的是這樣一個數列：0、1、1、2、3、5、8、13、21、34、……在數學上，斐波納契數列以如下被以遞歸的方法定義：  
      F（0）=0，F（1）=1，F（n）=F(n-1)+F(n-2)（n≥2，n∈N*）
  
  
#include<iostream>
using namespace std;
//遞歸形式
//long long  fibonacci(int i)
//{
//	return i < 2 ? i : fibonacci(i - 1) + fibonacci(i - 2);
//}
void test1()
{
	cout << fibonacci(6) << endl;;
}
//非遞歸形式
long long fibonacci(int n)
{
	int tem[2];
	tem[0] = 1;
	tem[1] = 1;
	if (n == 0)
	{
		return 0;
	}
	if ( n == 1)
	{
		return 1;
	}
	else
	{
		for (int i = 2; i < n; i++)
		{
			int temp = tem[0] + tem[1];
			tem[1] = tem[0];
			tem[0] = temp;
		}
		return tem[0];
	}
}
//優化    時間複雜度O（n）
long long fibonacci(int n)
{
	long long fibonacci[3] = { 0, 1, n };
	for (int i = 2; i <= n; ++i)
	{
		fibonacci[2] = fibonacci[1]+fibonacci[0];
		fibonacci[0] = fibonacci[1];
		fibonacci[1] = fibonacci[2];
	}
	return fibonacci[2];
}
int main()
{
	test1();
	system("pause");
	return 0;
}

     

我們不難發現在這棵樹中有很多結點會重複的，而且重複的結點數會隨着n的增大而急劇增加。這意味這計算量會隨着n的增大而急劇增大。事實上，用遞歸方法計算的時間複雜度是以n的指數的方式遞增的.

         在分析算法的時間複雜度的時候，我們也可以得到相同的結果，非遞歸使用的是for循環，其時間複雜度爲O(n)。而遞歸的時間複雜度則比較複雜，其分析出來爲O(2^n)。

         這裏需要說明的就是，非遞歸的for循環其時間複雜度O(n)雖然很小，但是其空間複雜度缺比遞歸調用差得多。因爲，for循環在每次循環的時候，都把相應的數值保存下來了，而遞歸調用卻不會保存相應的數值。