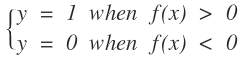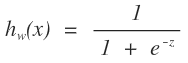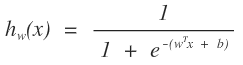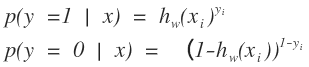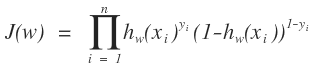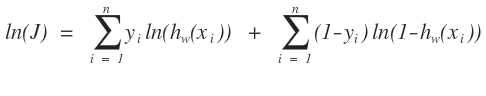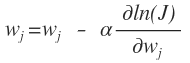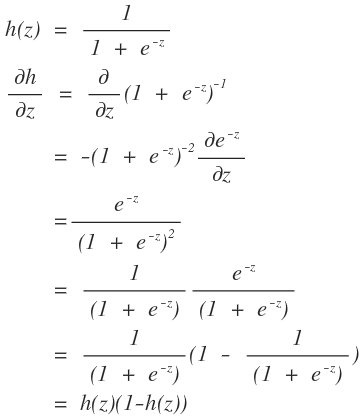摘要
邏輯迴歸是用在分類問題中,而分類爲題有存在兩個比較大的方向:分類的結果用數值表是,比如1和0(邏輯迴歸採用的是這種),或者-1和1(svm採用的),還有一種是以概率的形式來反應,通過概率來說明此樣本要一個類的程度即概率。同時分類問題通過適用的場合可以分爲:離散和連續,其中決策樹分類,貝葉斯分類都是適用離散場景,但是連續場景也可以處理,只是處理起來比較麻煩,而邏輯迴歸就是用在連續特徵空間中的,並把特徵空間中的超平面的求解轉化爲概率進行求解,然後通過概率的形式來找給出分類信息,最後設置一個閾值來進行分類。
邏輯迴歸
問題描述
首先我們要明白,我們要解決的問題:給你一批數據,這一批數據特徵都是連續的,並且我還知道這批數據的分類信息(x,y),x爲特徵,y爲類別,取值爲:0或者1。我們想幹什麼,想通過這批數據,然後再
給一個新的數據x,這個數據只存在特徵,不存在類別,我們想給出分類的結果,是0還是1。下面爲了方便,我們以二維空間的點爲例進行說明。
解決策略
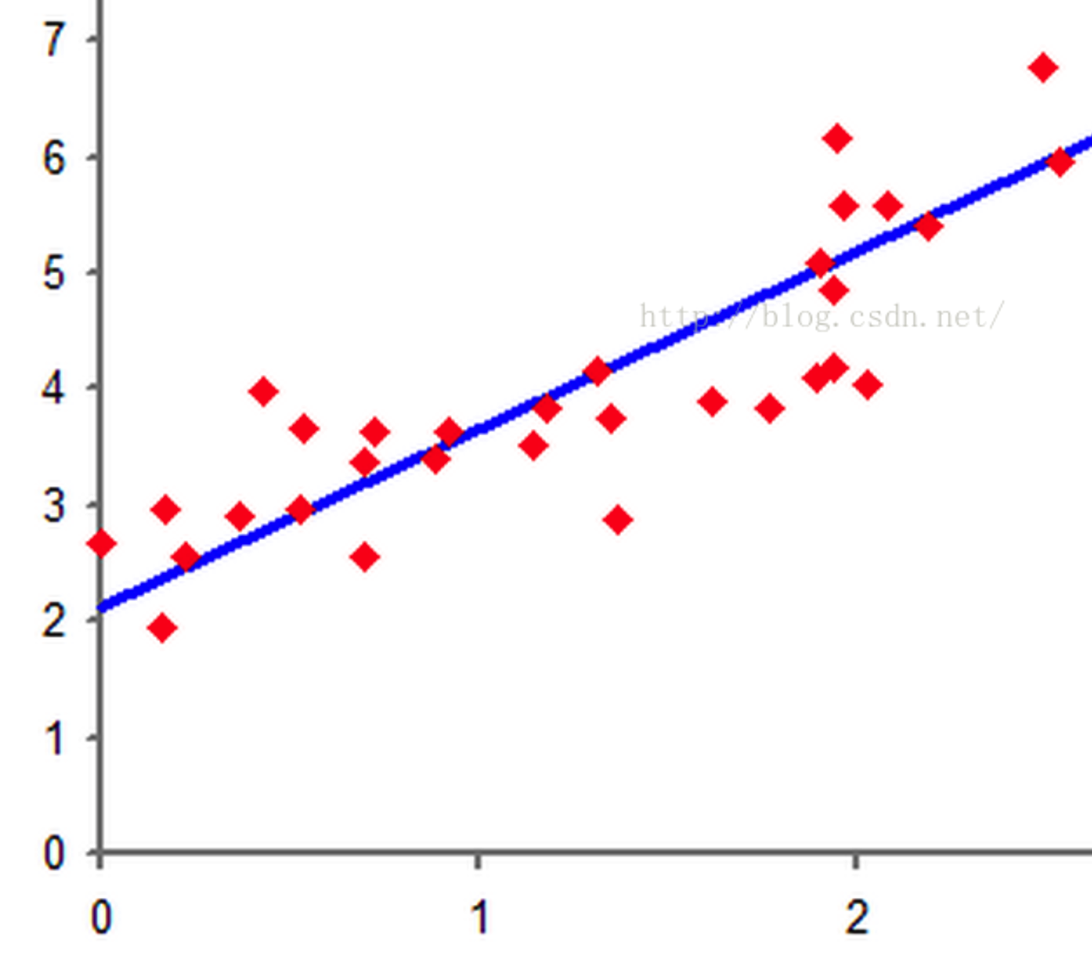
遇到這個問題時,我們首先做的是把數據的特徵放到空間中,看有沒有什麼好的特點。如下,從網上取的圖。
這些是二維空間的點,我們想在空間中找到一個超平面,在二維空間中超平面的爲一條直線f(x),當我們帶入數據時:
就是我們所要求的的直線。那麼找這個直線怎麼找,在機器學習中,我們要找的是一個學習模型,然後通過損失函數來進行模型參數的求解。那麼對於邏輯迴歸,求邏輯迴歸的參數就是w和b,那麼這個損失函數應該怎麼設置。給一條數據,我們希望,他距離這個直線越遠我們越可以認爲能夠很好的進行分類,即屬於這個類的可信度就越高。那麼我們就需要有一個函數來反應這個情況啊,古人也很聰明啊,使用了logistics函數:
而且這個函數又非常的好,f(x)來衡量數據距離超平面的距離二維中是直線,他被成爲函數間隔,f(x)是有正負的,上圖中,在直線上面的點發f(x)是負的,相反位於其下的點事正的。這個爲什麼?是解析幾何的最基本的一些性質了。
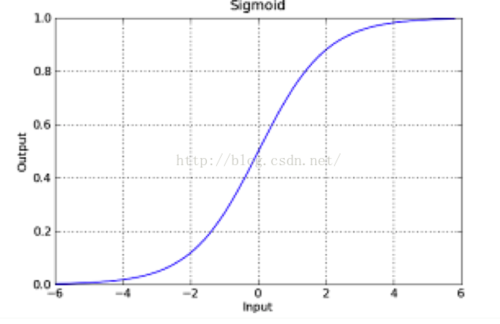
是直線,而不在這個直線上的點f(x)是帶入後,其實是不等於0的,但是有規律,則就可以通過這個規律來進行劃分分類。以上面的圖爲討論對象,位於上方的點是負的,爲與下方的點是正的,那麼當f(x)爲正,越來越大,則說明點在直線的下方越來越靠下,那麼他分爲一個類的可能性是不是越大啊,相反,在上方的時候,f(x)是負的,越來越遠的時候,是不是越靠近另一個類啊。那麼logistics函數不就是反應了這個現象嗎?我們類別設置成0或者1,當f(x)正向最大時爲1,f(x)負向最大時爲0,多好。下面給一下logistics的圖像(網上盜圖):
這個函數是不是可以反應出我們所說的情況。其中f(x)就是我們logistics函數的x軸的值。y可以是一個程度,h越大,則說明其分爲正類1的可能性越大,h越小,則說明分爲負類0可能性越大。那麼在數學中可能性的度量是什麼?概率啊,logistics函數的大小剛好是[0,1]之間的,多好啊。那麼我們以前的求直線問題就轉化爲求如下的函數:
把以前的問題就轉化爲求概率的問題
爲什麼把y放上面,我認爲這只是數學上的一種表示形式,給一個特徵樣本,要麼屬於0類的,要麼屬於1類的,在不知道的情況下這樣表示和最後知道類別得到的概率是一樣的嘛。變化後的logistics函數其中的參數也只是包含w和b,那麼我們求解超平面轉化爲了求解h函數,在概率問題中,求解最優化的損失函數是誰?這又涉及到另外一個問題,我的數學模型已經有了,數學模型中包含一些參數,我需要進行抽樣,得到這個問題的一些樣本,理由這些樣本來對參數進行估計,對參數估計時需要一個損失函數。概率問題最優化的損失函數一般用的是最大似然函數,也就是通過最大似然估計進行計算。這樣大家又會問,最大似然估計最大化的是什麼?只有知道最大化的是什麼的時候,我們才能構造出似然函數啊。剛纔我們說了進行參數估計時,我們需要一個樣本,那麼最大似然函數最大化的是這個樣本出現的概率最大,從而來求解參數。可能有點抽象,在樣本空間中,樣本空間的數據很大,我們想得到含有n個對象的樣本,這樣含有n個的樣本是不是有很多很多,不同的人得到的樣本數據也不一樣,那麼在我們已經得到了這n個樣本的情況下,我們進行參數估計,最大似然估計最大化的是我們已經得到的樣本在整個樣本空間中出現的概率最大,從而來求解參數。
最大似然估計
通過上面的討論,我們很容易構造出我們的似然函數:
這就很簡單了,把上面的似然函數對數化,即:
一般有數學基礎的人都會知道我們這個下面就是求導唄,現在的x和y都是已知的只有w是未知的,我們要求的是找到w是我們抽到這個樣本的概率最大。但是有一個問題,這樣平白無故的求的w不一定是我們這個樣本中最優的啊,不是讓我們在整個樣本空間中進行求導,而是我們有一個樣本,在這n個樣本中找到我們最想要那個的w,這個用什麼啊,這種搜索算法最常用的就是梯度下降啊,沿着梯度的負方向來找我們想要的點。
1、圖中的i表示的是第i個記錄,j表示的一個記錄中的第j個特徵分量
2、上面的推導中1→ 2爲什麼有求和,而後又不存在了啊,這個是和梯度下降法有關係的,梯度下降法就是在當前點下找到一個梯度最大的點作爲下一個可以使用的,所有在1到2中,去掉了求和號
3、2→ 3的推導是根據logistics函數的性質得到的。
如果這還是不懂,那沒有辦法了。