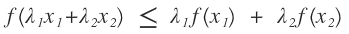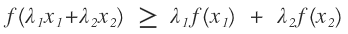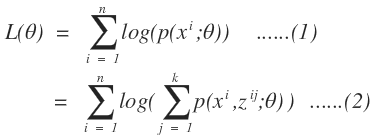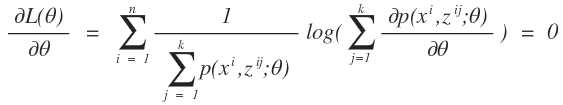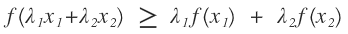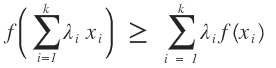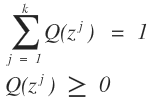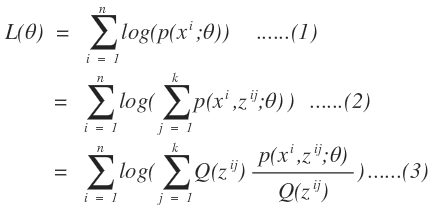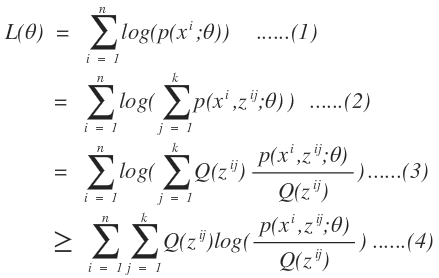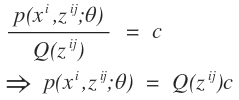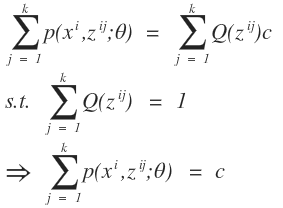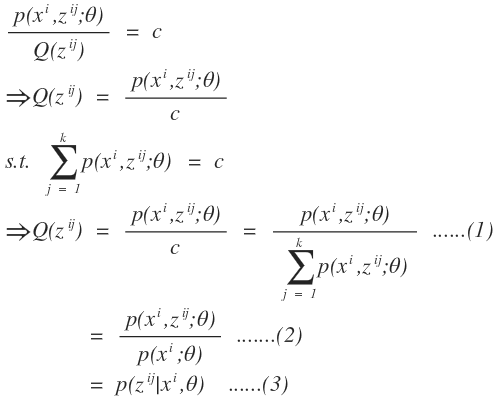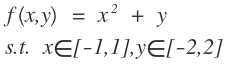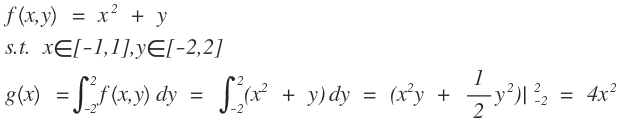摘要
EM算法主要分爲兩個步驟:E-step和M-step,主要應用在概率模型中。機器學習中,概率模型在進行參數估計時,我們主要應用的是最大似然估計,所以在對EM算法進行討論時,是離不開最大似然估計的。EM算法主要是用來解決那些樣本中存在隱變量的情況。E-step固定模型參數通過數學模型求解隱變量,M-step根據E-step求得的隱變量在通過最大似然估計最大化似然函數從而求出模型的參數,這樣相互的迭代,從而得到模型的局部最優解。EM算法主要應用在聚類算法中,因爲一般情況下聚類問題都存在一個隱變量。
什麼是隱變量
樣本中存在隱變量即我們在對數據進行採樣中,可以認爲隱變量是那些我們不能通過數據採樣所能確定的屬性。如果不存在隱變量,那對於一些聚類模型,我們的參數求解就簡單很多,比如k-means,k-means只是利用了EM算法的思想。我們有一批數據,想利用k-means算法來進行聚類分析,對於k-means算法,我們要確定的是k和k個質心,假如我們在對這批數據採樣時已經知道他們分爲4類,而且採樣前就已經把數據給分好類了,已經知道了,還用聚類算法幹嘛,我們這是暫時的假設用他來舉例說明什麼是隱變量,那麼我們在用k-means算法時就變得很簡單了,直接求出這k個質心,而不用我們所熟知的k-means算法的計算步驟。之所以我們使用我們所熟知的k-means算法的步驟,那是因爲我們不知道每個樣本應該歸屬於哪個類以及他們存在多少個聚類中心比較合適。那麼這個隱變量就是每一個樣本應該歸屬於哪個類。在舉一個例子,高斯混合模型,這個是典型用到了EM算法的思想,如果對這個模型不太清楚,可以網上查資料。同樣,我們也有這樣一批數據,在採樣中,我們就已經知道k和每個樣本應該屬於哪個類,那麼我們所要做的工作就是把每一類數據拿出來,直接通過均值和方差就可以求出每一個高斯函數的模型了,而不需要再進行EM算法通過最大似然估計來計算我們的高斯混合模型參數了。而現實的應用中是我們不知道這樣的一批數據應該分爲幾個類以及每一個樣本應該屬於哪一個類,那麼這就是隱變量。這樣的問題和先有雞還是先有蛋的問題差不多,當我們知道數學模型的參數後,我們就知道了樣本應該屬於哪個類,同時當我們知道隱變量後,我們也就知道樣本屬於哪個類,從而得到數學模型的參數,但是不幸的是在開始的時候我們只有樣本,隱變量和模型參數都不知道。
凸函數和凹函數以及其性質
爲什麼要講這個,因爲EM算法得以實施的基礎就是函數的凹凸性以及凹凸函數的一些性質。所以這裏還是說一下吧。
在高等數學和數學分析(數學專業的書)對於凹凸函數的定義可能有些不一樣。這個沒有關係只是叫法不同,但是他們這些圖形和圖形的性質是一樣的。
凸函數定義:函數的二階導函數在一定的區間內大於等於零,性質如下
如下圖:
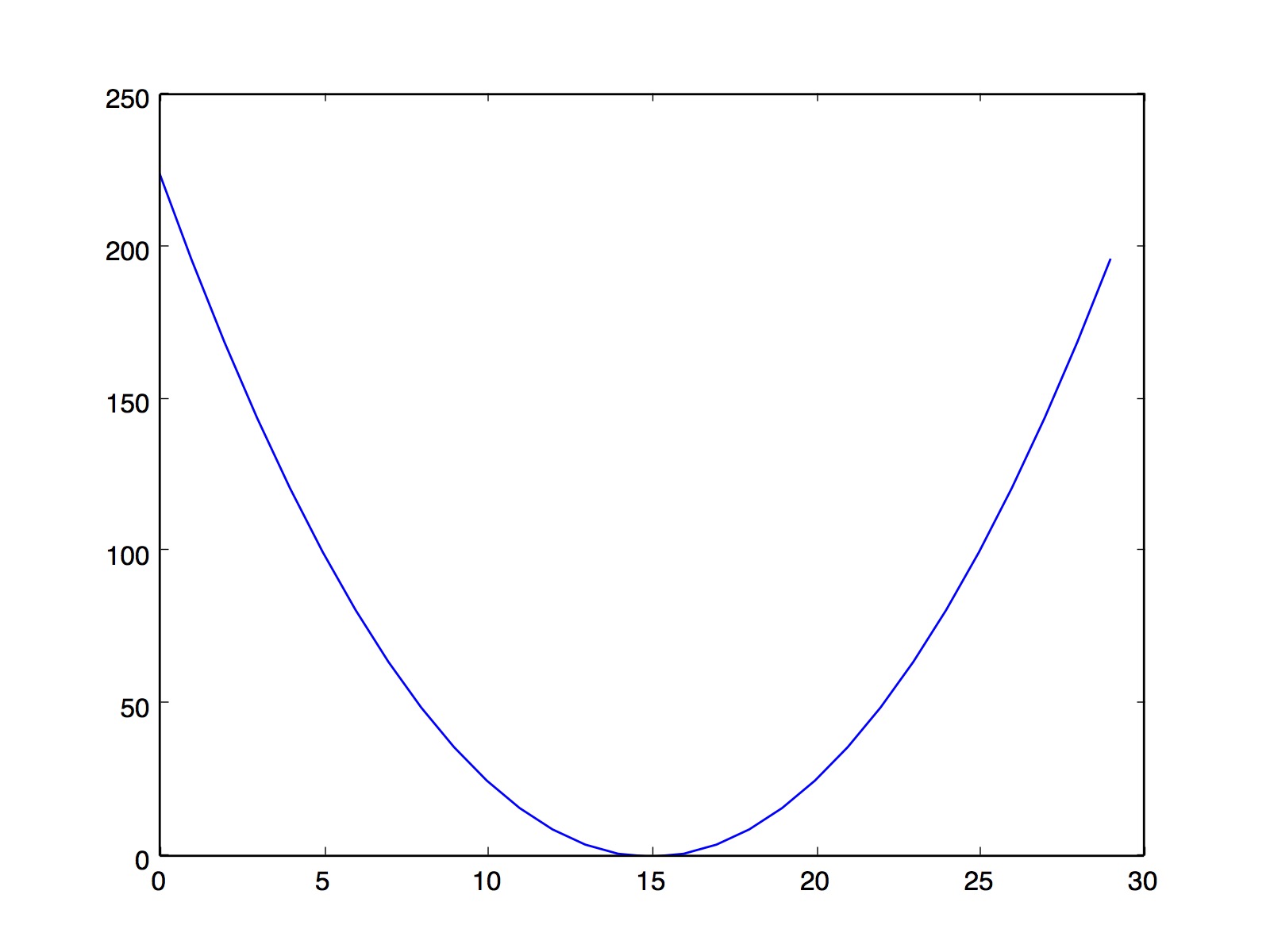
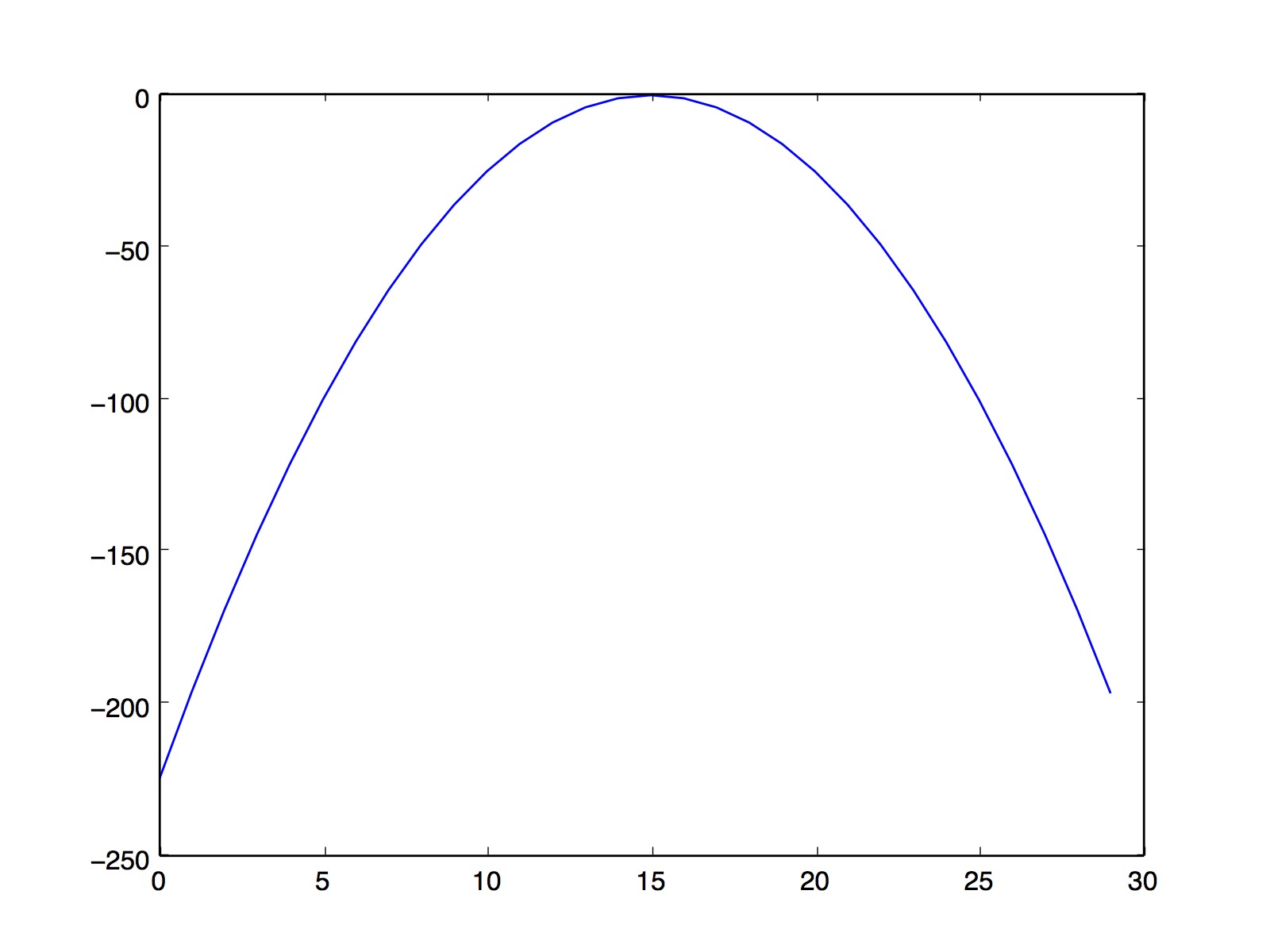
凹函數的定義:函數的二階導函數在一定的區間內小於等於零,性質如下:
如下圖所示:
最大似然估計步驟
因爲在概率模型中,進行參數估計一般都採用最大似然估計
1、確定概率模型求出似然函數
2、對似然函數取log,把連乘變爲求和
3、對變換後的似然函數求導,並另導數等於0,然後整理得到似然方程組
4、求解似然方程組,得到模型參數
EM算法
假設我們有一批數據樣本{x(1),…,x(n)},,樣本容量爲n,概率模型爲p(x,z)來對我們的數據進行擬合。根據概率模型的參數估計算法,我們可以得到似然函數:
上式中(1)我們是通過最大似然估計的步驟獲取的,從(1)到(2)引入了樣本屬於某一個類的概率函數,從而對某一個樣本求得該樣本屬於某個類的全概率公式,即引入了隱變量z。
當我們採用傳統的概率模型求解參數的方法即最大似然估計,對上述式子進行求導數,從而得到似然方程:
我們會發現上述似然方程中存在對數,並且對數裏面是個求和公式,這種求解是很難得到參數的解析解的。遇到衚衕了,我們就要想一下拐一下彎,既然這個公式無法求解的難點在於對數裏面有求和公式,那麼我們能不能採用什麼辦法把對數後面的求和號給拿到外面。再看看對數函數的性質是什麼樣子的?對數函數是一個凹函數那麼他肯定滿足凹函數的基本性質:
把上式進行變換:
我們的目標函數和凹函數的性質還差那麼一點點的差距,那麼我們就認爲對於每一個實例i,用Qi表示對應於隱含變量即其屬於哪個類的概率分佈,我們這是對於一個樣本而言的,那麼樣本有n個,就會存在n個這樣的Qi的函數分佈,一定要把這一點弄明白。這個Qi表示的樣本i對應於k個類,其屬於這k個類的概率分佈。那麼Qi應該滿足的條件是:
那麼我們就可以把我們的似然函數進行改寫了:
這樣一看就和我們的凹函數性質一致了吧。於是我們可以把上述函數通過凹函數的性質進行變換:
既然原函數無法得到最優解,我們可以通過調整原函數的下界函數,對原函數的下界函數求最大值,從而使原函數逐步逼近最優解或者得到一個局部最優解。即我們不停的求解上式中(4)的最大值,從而是我們原函數逼近最優解。
看到這可能會有一個問題,通過最大似然估計得到的原似然方程無法得到解析解,爲什麼變成(4)就可以得到了呢?我們在已知隱變量的前提下對模型參數進行求偏導得到的似然方程中,發現log已經不復存,已經變成了我們熟悉的線性方程組或者非線性方程組(這個跟數學模型有關),一般情況下這個就可以利用線性代數的理論進行求解了啊。
因此EM算法的基本思想就是通過引入隱變量,先得到樣本屬於某一個類的概率,然後再使用最大似然估計最大化似然函數來求解參數,得到參數以後,數學模型就已經確定,那麼我就可以得到樣本屬於哪個類了,從而得到隱變量的值,因此就用迭代的進行求解最終得到問題的解。當我們引入隱變量後,整個似然函數就會存在兩類參數類型:隱變量和數學模型的參數。那麼EM算法採用的步驟如下:
E-step: 通過固定數學模型的參數,利用現有樣本對隱變量進行參數估計,即求出隱變量的期望也就是我們期望樣本屬於哪一個類
M-step: 通過E-step求得的隱變量,對數學模型參數求導,最大化似然函數。
隱變量的求解
對於EM算法,我們是不斷的逼近最優值,那麼E-step計算的是什麼呢?因爲在凹函數的性質中上述不等式取等號的前提條件是xi爲常數
則:
對上式進行求和:
通過上述兩個式子我們進行變換得到:
在上式中從(1)到(2)爲什麼會是這樣,我們按照舉個例子,用二元一次函數的積分問題來看待這個問題的推導,因爲積分的實質也是一種求和對函數下部的面積進行無線的拆分然後再求和。如下式的二元函數:
然後我們對上面的二元一次函數對y進行求積分:
從而消除了變量y,同樣的道理,從(1)到(2)的過程中,我們分母對樣本i的所有的可能隱變量取值求和,從而把隱變量z給消除,從而得到公式(2)從(2)到(3)是通過條件概率的公式得到的。因此我們可以發現隱變量其實就是在固定數學模型參數和已知數據樣本的情況下的後驗概率。
以上只是理論部分,下面我們簡單說一下EM算法的實際應用。
在實際應用中我們不會按照上面公式來推導我們的算法。我們只知道兩個點就可以了:隱變量的求解和已知隱變量的前提下最大化似然函數從而來求解數學模型的參數。
隱變量的求解:我們已經知道其是樣本和數學模型參數的後驗概率,那麼我就可以根據實際的情況來推導計算這個後驗概率從而得到我們的隱變量和參數的關係表達式從而用於迭代求解即爲E-step
最大化似然函數:這個是我們最大似然估計算法的步驟了即M-step。
---能力有限,存在不對的地方,望請指教。