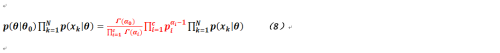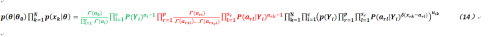前言
貝葉斯決策可能在相關機器學習或數據挖掘或專家系統中有着廣泛的應用,故其地位也相當重要;比如在垃圾郵件的過濾、釣魚郵件的判定、垃圾(釣魚)短信過濾等場合的應用就相當多(因爲筆者較多地從事這些工作),或者可以說上述這些應用其實其主要方法就是使用了貝葉斯方法(當然也可以混合使用其它方法,比如支持向量機);在信息安全中,貝葉斯決策就是一個二分類問題(即是存在惡意或不存在惡意),而應用在其它場合肯定還存在多分類的問題,當然本文主要討論的是其通用方法,所以是建立在多分類的基礎上,或者說我們討論的是貝葉斯分類。
貝葉斯決策與另外一個被稱作貝葉斯網絡的東西有一定聯繫,因爲它們都是基於貝葉斯方法,而不是什麼其它的方法,但後者的應用場合主要是:
原因診斷:即求在網絡中子節點發生某一狀況時,父節點發生的可能性;
因果預測:這個和上述情況相反,即求在父節點發生某種狀況時子節點發生的可能性;
解釋遠離:即當影響到結果(子節點)的原因多於一個時,結果與其中一個原因發生的條件下,另一個或幾個原因不發生的可能性。
所以通過上面的表述可以看出,貝葉斯決策和貝葉斯網絡(又被稱爲信念網絡,即Belief Network,稍作改變就成爲深度信念網絡,即DBN)的應用場景有着顯著的不同,而且它們訓練的方法也存在差異,後者一般使用蒙特卡洛方法(準確地說是MCMC方法,即對各隨機變量依次進行抽樣)訓練,本文並不涉及任何有關貝葉斯網絡的內容,特此說明。
預備知識
從以前一般機器學習的套路看,我們總是給出一個目標函數,然後對其進行最大化(也有可能最小化,比如加一個負號,或者其它對偶的處理方式,如分子變分母或者應用相反的操作,這個在支持向量機的推導中會被應用到),但我們之前最常用的方法、或者說幾乎是唯一的方法就是使用最大似然估計(當然目標中含有參數需要確定,如果是基於無參的方法,比如山峯聚類,則不然),那麼還有什麼其它方法?或者說最大似然估計可能還存在什麼解決不了或不完全適用的問題?
回答是肯定的,因爲我們在用大量樣本求解目標函數的最優解過程中,可能存在一個蠻自然的想法就是這些個被求解的參數(比如高斯分佈中的均值、方差,多項式分佈中的各個類的抽樣概率)是不是可能也滿足某種分佈?而且確實人們在認識某事物的時候,開始可能有個先驗的概念,但隨着慢慢地深入下去,認識也可能在慢慢地改變(難道這個是辯證法的具體體現?),故討論參數的分佈狀況也就成爲必然,而這種對參數分佈進行研究和估計的方法就被稱作貝葉斯估計,本節主要討論兩種貝葉斯估計方法,其一是基於高斯密度的貝葉斯估計,而另外一個則是n元多項分佈的貝葉斯估計,它們將成爲我們具體討論貝葉斯決策(其實是樸素貝葉斯)的實現工具(主要是後者)。
先給出相關貝葉斯估計的基礎公式:
我們的目標就是要最大化公式1,通過觀察可以發現,其實它和之前使用的最大似然估計只是多了一個對參數分佈的概率,而則是參數初始的狀態,明白了這一點那麼理解下面的推導就不是非常困難了,僅僅是又繁瑣了一點。
高斯密度的貝葉斯估計
在基於高斯密度的貝葉斯估計中,我們設定參數的分佈如下式:
如果讀者熟悉最大似然估計的公式,可以比較一下上述公式與其區別,其實也就是均值的估計形式(在最大似然估計中,均值就是簡單的求和併除以樣本數量而已)不太一樣,而對於方差參數的估計是一模一樣的。
至此我們已經討論完了基於高斯密度函數的貝葉斯估計。
n元多項式的貝葉斯估計
那麼對於n元多項式的貝葉斯估計有什麼不同呢?或者換言之,在n元多項式中,參數指的是什麼?先給出n元多項式的概率分佈公式(實際上是樣本的概率分佈,而參數的分佈有點不同):
這個是什麼意思?我們假定x只能取1,2,...,c其中之一,而就是相關參數(即取每個值的概率,顯然它們的和等於1),它的指數部分只能取0或者1,而且取0或1之間是互斥的,換言之就是
,另外還有如下的約束:
。
根據公式1和公式7,我們可以得出n元多項式的貝葉斯估計的目標函數(好拗口):
對於上述公式而言,可能乘積的第一部分(被標爲紅色)有點疑惑,其實它就是狄利克雷分佈(一個被稱作“分佈的分佈”的神奇的分佈,它和多項式分佈有着天然的關係,可以理解它就是伯努利分佈的多值情況推廣,一種較爲通用的分佈表達形式,相關內容可以參看網上的介紹,這裏不再囉嗦;Gamma裏面的參數是希臘字母Alpha,不是英文字母a)。
按照老辦法,我們對公式8取對數可得如下公式:
貝葉斯決策
一個例子
在討論貝葉斯決策之前,爲了直觀起見我們先看一個例子(筆者也無意多找其它的樣例,這個例子就是來自於於劍的《機器學習:從公理到算法》一書,能簡單明瞭地說明問題即可),下表是一個名詞性數據集,每個樣本包含5個特徵和一個樣本類別標記:
特徵F1的取值範圍爲{s,o,r}
特徵F2的取值範圍爲{h,m,c}
特徵F3的取值範圍爲{h,n}
特徵F4的取值範圍爲{t,f}
特徵F5的取值範圍爲{d,r}
而每個樣本被分爲L1和L2兩個類別。
現我們有20個樣本,其各個特徵的取值和分類情況,如下表所示:
序號 | F1 | F2 | F3 | F4 | F5 | 類別 |
1 | s | h | h | f | d | L2 |
2 | s | h | h | t | d | L2 |
3 | o | h | h | f | d | L1 |
4 | r | m | h | f | d | L1 |
5 | r | c | n | f | d | L1 |
6 | r | c | n | t | d | L2 |
7 | o | c | n | t | d | L1 |
8 | s | m | h | f | d | L2 |
9 | s | c | n | f | d | L1 |
10 | r | m | n | f | d | L1 |
11 | s | m | n | t | r | L1 |
12 | o | m | h | t | r | L1 |
13 | o | h | n | f | r | L1 |
14 | r | m | h | t | r | L2 |
15 | r | m | n | f | r | L1 |
16 | s | m | n | t | r | L1 |
17 | o | m | h | t | r | L1 |
18 | o | h | n | f | r | L1 |
19 | r | m | h | t | r | L2 |
20 | r | c | n | t | r | L2 |
如果需要計算新的樣本x={s,m,h,t,d}的分類,那麼該如何利用上表中給出的樣例進行劃分?
根據上表我們可以得到如下若干個條件概率(暫使用(x)i來表示樣本x的第i個特徵),以下是關於各個特徵取值其被劃分爲類別L1的分佈情況:
P((x)1=s|L1)=3/13 P((x)1=o|L1)=6/13 P((x)1=r|L1)=4/13
P((x)2=h|L1)=3/13 P((x)2=m|L1)=7/13
P((x)2=c|L1)=3/13
p((x)3=h|L1)=4/13 P((x)3=n|L1)=9/14
P((x)4=t|L1)=8/13 P((x)4=f|L1)=5/13
P((x)5=d|L1)=6/13 P((x)5=r|L1)=7/13
而根據上表,我們則也能夠得到在各個特徵不同取值的情況下,被劃分爲類別L2的概率:
P((x)1=s|L2)=3/7 P((x)1=o|L2)=0 P((x)1=r|L2)=4/7
P((x)2=h|L2)=2/7 P((x)2=m|L2)=3/7 P((x)2=c|L2)=2/7
p((x)3=h|L2)=5/7 P((x)3=n|L2)=2/7
P((x)4=t|L2)=4/7 P((x)4=f|L2)=3/7
P((x)5=d|L2)=4/7 P((x)5=r|L2)=3/7
需要說明的一點是,上面相關條件分佈概率中,被標爲紅色的一項在原書中是錯誤的,應該是4/7而不是5/7,否則在特徵4在不同取值情況下其被定爲類L2的條件概率之和就不是1,這個是不正確的。
那麼現在來看新的樣本應該被劃分爲哪個類別(其實就是計算它被劃分爲類別L1的概率大還是被劃分爲L2的概率大),我們有樣本被劃分爲L1的概率:
P(L1)*P((x)1=s|L1)*P((x)2=m|L1)*P((x)3=h|L1)*P((x)4=t|L1)*P((x)5=d|L1)=(13/20)*(3/13)*(7/13)*(4/13)*(5/13)*(6/13)=126/(13*13*13*13)
而樣本被劃分爲L2的概率如下:
P(L2)*P((x)1=s|L2)*P((x)2=m|L2)*P((x)3=h|L2)*P((x)4=t|L2)*P((x)5=d|L2)=(7/20)*(3/7)*(3/7)*(2/7)*(4/7)*(4/7)=72/(5*7*7*7*7)
同樣的原因,上面概率的計算在原書中實際上是錯誤的(也被標爲了紅色,供讀者進行印證),不過基本不影響計算結果的比較。通過比較上述兩個概率大小,我們能夠得到結論,x應被劃分到類L2。至此我們大致對於貝葉斯決策的原理和分類過程有了一個初步的印象。
但若給定的樣本是x=(o,m,n,t,r),則該如何得到其類標呢?因爲其中x的第一個特徵取值是o,而在樣本中並無此例子(概率是0),故它永遠不會被劃分爲類L2,這個在現實處理中總是存在一定問題,針對這種情況,我們在稍後的部分予以討論。
貝葉斯決策的最大似然估計
在本文的前面部分曾經說過,一般而言我們對於相關參數的估計有兩種方法,現在本節主要討論如何利用最大似然估計(可以結合上例)來處理貝葉斯決策問題。
由最大似然估計的一般理論我們有如下公式:
說實話上述公式比較複雜(可能貝葉斯估計的公式更加複雜),這裏有必要解釋一下。首先在上式中最外兩個連乘符號應無疑義,分別是樣本的個數以及樣本的分類個數(就是c,這個和預備知識中所涉及的c略微不同,但符合我們其它文章中的相關符號表示);而括號中的兩個連乘符號則分別表示在一個樣本中,其不同維度(維度爲p)的可能取值數量(即對於維度r,其相應維度的可能取值數量最大爲個,也就是其集合的範數,這裏討論的是離散情況,如果取值是連續的呢?);另外
的含義不用過多介紹了,這個在其它文章中已經不止一次地給出,而
又是什麼鬼?這個被稱作Kronecker函數,其含義爲如果括號中的兩個值相等則函數值爲1,否則爲0,解釋完畢。
根據公式13,我們可以得到如下的相關公式:
讀者可以將公式12和公式13和上節給出的例子進行印證,能夠看出確實如此。
貝葉斯決策的貝葉斯估計
而如果使用貝葉斯估計會有什麼不同呢?根據公式1以及公式8給出的結論,我們可以得到如下公式(理解這個公式需要看清楚不同的部分,筆者用了不同的顏色進行標註):
這個公式可能是目前最長的,如何理解它?筆者使用了三種不同的顏色來標註,其中綠色和紅色的部分實際上就是參數的狄利克雷分佈,綠色可以理解爲類的分佈情況,而紅色部分則是每個維度存在不同取值的狄利克雷分佈(這個和n元多項式的貝葉斯估計略爲不同,原因是我們要處理多維情況),而黑色部分針對的是某個樣本被劃歸爲某個類以及對某維度取值的估計,這個部分和最大似然估計沒有什麼太大區別。
通過對公式14的求解,我們能夠得到如下結果:
其中大於等於0,當其爲0時,貝葉斯估計退化爲最大似然估計,而其取1時,貝葉斯估計變爲拉普拉斯平滑(Laplace Smoothing),使用拉普拉斯平滑的好處在於如果樣本集中有某些特徵取值爲0,那麼通過這個變形可以避免其概率爲0的情形出現。