同构和同态
在抽象代数中,同构指的是一个保持结构的双射。在更一般的范畴论语言中,同构指的是一个态射,且存在另一个态射,使得两者的复合是一个恒等态射。
在数学中研究同构的主要目的是为了把数学理论应用于不同的领域。如果两个结构是同构的,那么其上的对象会有相似的属性和操作,对某个结构成立的命题在另一个结构上也就成立。因此,如果在某个数学领域发现了一个对象结构同构于某个结构,且对于该结构已经证明了很多定理,那么这些定理马上就可以应用到该领域。如果某些数学方法可以用于该结构,那么这些方法也可以用于新领域的结构。这就使得理解和处理该对象结构变得容易,并往往可以让数学家对该领域有更深刻的理解。
利用Cayley定理:每个有限群G都与某个置换群同构,任何一个抽象群都可以找到一个具体的群与它同构,而每一个同构的群,除了元素的差别外,就其代数性质,即由代数运算而产生的性质来说,则是完全一致的。
由此在我们所涉及到的群,其实都可以通过同构方式将置换群转化为软件设计中所涉及到的任何群,因此我们针对其任何意义的群我们并非一定需要进行具体研究,我们可以通过对置换群这一研究较多的群进行挖掘就能够达到目标。同时通过此定理我们也可以看出,我们使用“置换”来作为基本的设计原理也有其规范正确的理论基础。
图的同构:假设G=(V,E)和G1=(V1,E1)是两个图,如果存在一个双射m:V→V1,使得对所有的x,y∈V均有xy∈E等价于m(x)m(y)∈E1,则称G和G1是同构的,这样的一个映射m称之为一个同构,如果G=G1,则称他为一个自同构。
同一座标结构概念的两组座标称为是同构的,如果它们具有同样的形状,更严格地说,两组座标同构的条件是存在它们之间的一个一一对应,使来自第一组中的一个遍历函数对座标的任何合法应用返回的座标,对应于同一个遍历函数作用于来自第二组里的那个对应座标得到的结果。
检查同构的算法只使用遍历函数,因此同构与被座标指向的对象的值无关,但同构要求同样的访问函数在对应的一对座标上或者都有定义,或者都无定义,例如,两个有界或计数范围同构的条件是它们的规模相同。
对双向二叉座标,树同构的体检是同时遍历得到相同的访问序列。
泛型编程其能够完成其泛化和特化的处理,就是因为针对此图的关系来说,其模板和特化的置换点局部上具有同构的关系结构,只有这样才能够进行泛型化的编程。如图2-8所示比较形象的表示这样的置换方式。
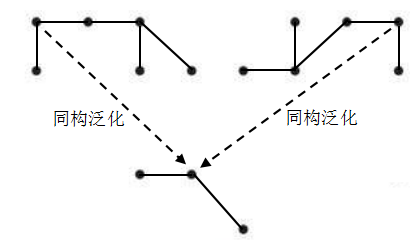
图2-8
2度顶点同构:
两个图G1和G2称为在2度顶点内同构的(或称同胚),如果它们是同构的,或者通过反复插入和(或)除去2度顶点,它们能变成同构的图。
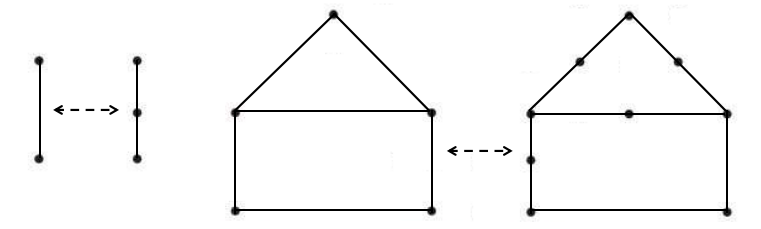
图2-9
所以,如果我们需要新增或重构设计进入原来的系统,那么采用的方式就是要求加入后的图与加入前的图保存2度顶点同构(如图2-9所示),这是耦合性最小的加入形式,也是系统保持优化和整洁的理论基础。从中可以看出,新增的置换点和相邻的置换点最好是形成线性化的结构是最佳的体现,所以线性化机制将变得异常突出。
同态:
假设M,M′是两个乘集,也就是说M和M′是两个各具有一个封闭的具有结合律的运算*与*‘的代数系统。σ是M射到M′的映射,并且任意两个元的乘积的像是这两个元的像的乘积,即对于M中任意两个元a,b,满足
σ(a*b)=σ(a)*’σ(b);
也就是说,当a→σ(a),b→σ(b)时,a*b→σ(a)*’σ(b),
那么这映射σ就叫做M到M′上的同态。
格同态:对于格<L,*,⊕>和格<S,∧,∨>,定义一个映射f:L→S,如果对于任何a,b∈L,有f(a*b)=f(a)∧f(b)和f(a⊕b)=f(a)∨f(b),则称f是从<L,*,⊕>到<S,∧,∨>的格同态。
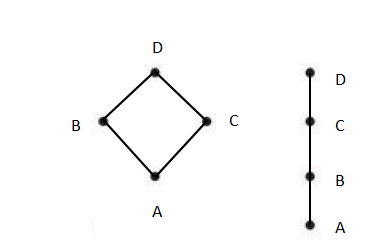
如果我们将继承和抽象关系形成的偏序格如下图所示,那么我们可以通过格同态转化为一个全序链,此就是表示菱形继承方式可以通过格同态转化为单链的继承结构,如图2-10所示。
图2-10
我们对同构和同态进行了数学方面的定义,其实我们就利用同构或同态能够辅助我们建构系列模型,利用这些系列模型能够将相似的模型进行对应,以此能够获取更大的相通性。让我们先来看看大师们是如何运用这一特性的。
香农认为,密码系统中对消息的加密变换的作用类似于向信息中存在的噪声。密文就相当于经过有扰信道得到的接收消息,密码分析员相当于有扰信道下原接收者。不同的地方在于,这种干扰不是信道中的自然干扰,而是发送者有意加进的,且可由己方进行设计和控制、选自有限集的强干扰,也就是密钥,其目的是己方可方便地除去发端所加的强干扰,从密文中恢复出原来的信息,而使敌方难于从截获的密报中提取出有用信息。所以密钥的随机性将成为关键所在。传信系统中的信息传输、处理、检测和接收过程,与密码系统中的加密、解密、分析和破译过程都可用信息论观点统一地分析研究。密码系统本质上也是一种传信息系统,是普通传信系统的对偶系统。
香农以概率统计的角度对消息源、密钥源、接收和截获的消息进行数学描述和分析,香农深刻揭示了冗余度在密码中的作用,用不确定性和唯一解距离来度量密码体制的保密性,深入阐明了密码系统、完善保密性、纯密码、理论保密性和实际保密性等重要概念,从而大大深化了人们对于保密学的理解。这使信息论成为研究密码学和密码分析学的一个重要理论基础,将密码学从艺术变成了科学,宣告了科学的密码学时代的到来。