代數結構
線性序:
設集合X上有一全序關係,如果我們把這種關係用 ≤ 表述,則下列陳述對於 X 中的所有 a, b 和 c 成立:
ü 如果 a ≤ b 且 b ≤ a 則 a = b (反對稱性)
ü 如果 a ≤ b 且 b ≤ c 則 a ≤ c (傳遞性)
ü a ≤ b 或 b ≤ a (完全性)
配對了在其上相關的全序的集合叫做全序集合、線序集合、簡單序集合或鏈。
在數據結構中,單鏈表就是具有這樣的全序關係的集合,只是單鏈表是體現在數值是類結構對象上,而我們的接口(編程語言中特定化的接口)是最體現線性序的顯著特徵,其實本可以選擇其他的結構形態的,例如採用樹、hash表等等來表示,但是,選擇線性序是最爲簡單有效的處理方式,接口中不同的置換點通過一種最爲鬆耦合的方式結合在一起,不同的置換點是獨立的(無自反的關係、非對稱的雙邊關係),其關係僅爲相鄰(所以接口常常選擇函數指針類型的數組表示),由於採用這樣的最爲簡單構建方式,所以其實現處理也是簡單有效的,同時越是最特殊的結構,其特徵就最爲豐富,其變化也才最爲廣泛。
但是,對於一些結構化的非線性序的結構,其實我們也可以設置一些標誌,通過在訪問方面的過程,將這些結構進行線性序方式的訪問。例如在樹結構中我們可以使用先序、中序、後序的不同訪問方式,將樹進行了一個線性序的處理,這有助於轉換相關的問題來簡化我們的整個設計的複雜度。
羣:
任一集合A到自身的映射都叫做A的一個變換,如果A是有限集且變換是一一變換(雙射),那麼這個變換爲A的一個置換。有限集合A的若干個置換若作成羣,就叫做置換羣。
循環置換是置換的另一種表達形式,它以發生變化的文字的變化次序爲序,表 達成輪換的形式。每個循環置換都可視爲一個首尾相接的圓環。
兩個不相連的k—循環置換是可以交換的。
循環羣:設<G,*>爲羣,若在G存在一個元素a,使得G的任意元素都由a的冪組成,則稱該羣爲循環羣,元素a稱爲循環羣G的生成元。
一個質數階的羣必定是循環的,並且任一與幺元不同的元素都是生成元。
直積又叫笛卡爾(Descartes)乘積。設( G1,* )、( G2,· )是兩個羣,有各自的乘法 *、· 和各自的單位元e、l,分別從G1和G2中任取一個元素組成所有可能的有序對,組成的集合記作G1×G2,在上面定義一個運算◎,對於G1×G2中任意兩個元素(a1,B1)、(a2,B2),規定(a1,B1) (a2,B2)=(a1 * a2,B1 · B2),這叫做G1和G2的直積,記作{ G1×G2, ◎ },單位元是(e,l)。
G是交換羣的充分必要條件是G1與G2都是交換羣。
通過前面我們知道的三個羣,G1(值-地址置換、地址-值置換、賦值置換)、G2(抽象置換、繼承置換、類自反置換)、G3(泛化置換、特化置換、模板自反置換)其實都是3階的羣,然後根據置換的定義,這三個羣都是3階循環置換羣,其滿足了所有3階循環置換羣的所有特性。
通過將兩個羣進行直積,比如我們在面向對象的軟件設計中,我們所使用的正是上面的G1(值-地址置換、地址-值置換、賦值置換)和G2(抽象置換、繼承置換、類自反置換)的直積,當然,在這些對應的操作中可能存在有些置換操作是沒有的,因爲都作爲默認的處理,特別的這裏就存在接口來說,其由於沒有地址,所以無法進行地址和值的轉換操作,但是可以用於多態方式的賦值置換,同時其無法再進行抽象置換,只能夠進行繼承置換,所以其應該是<賦值置換,繼承置換>形成的置換對能夠滿足接口的置換動作。
自同構羣:
自同構羣是重要的幾何變換羣。是幾何學分類的依據。
設S是給定的空間,U是S上的一個圖形,若S到自身的一個變換g把U變到U自身,則稱g是關於U的自同構變換,簡稱關於U的自同構.S上關於U的自同構變換的全體構成一個變換羣,稱它爲關於U的自同構羣。在變換中保持不變的這個圖形U稱爲絕對形。
羣對於我們來說非常的重要,其所具有的特性讓軟件設計成爲了一種特殊的幾何或代數系統,而這裏需要明確的是,這裏不是所謂的幾何或代數的模型化,而是指其本身就是一種幾何和代數,這個結論對於我們進行深入分析非常必要的。
圖的自同構羣:
從圖G到其自身的一個同構稱爲是G的一個自同構,因爲映射的複合運算滿足結合律,恆等映射是一個自同構,一個自同構的逆任然是一個自同構,並且兩個自同構的複合也是一個自同構,所以圖G所有自同構的集合運算下構成一個羣,給羣稱爲是G的自同構羣。
因爲圖的每一個自同構都是頂點V(G)上的一個置換,所以用置換循環的術語可以更爲簡單地描述自同構。
對於圖G的頂點V,V通過G的自同構所映射到的頂點集合稱爲是G的一個軌跡。
由關係形成的不同等價類就是G的軌道,如果兩個頂點U和V屬於同一個軌道,則稱他們是相似的。
如果已知G中每個頂點的結構(軌道)信息,由於某些頂點的相似性,那麼就沒有必要去考慮G中所有的頂點,在此情形下,我們只需要考慮每個軌道的(任意)一個頂點,作爲該軌道的代表元,如果一個n階圖有n個不同軌道,那麼自同構羣僅僅由一個自同構組成,即恆等同構,另一方面,如果圖G僅有一個軌道,那麼G中任意兩個頂點都是相似的,此時我們稱G是頂點可遷的,因爲自同構只能把一個頂點映射到一個與它有相同度的頂點,所以每個頂點可遷圖是正規的。
我們的可置換點形成的關係絕大多數都是以圖的形式呈現,若非進行優化,其最初的形態絕大多數都是圖,對於圖的自同構來說,此爲一種特殊的圖,因爲頂點是相似的,所以可以將此頂點對應的置換點進行歸併處理,同樣能夠將此圖進行規範,更容易的轉化爲線性鏈的結構。
在軟件設計開發中,能夠獲得羣的集合和運算比較少,但是能夠形成半羣則是一個非常廣泛的概念,例如我們提到的G2(抽象置換、繼承置換、類自反置換)中,獨立出的繼承置換形成的集合S2(繼承置換)則具有半羣的系列屬性。
半羣由於其要求並不太高,所以我們的很多操作都可能形成半羣。而半羣由於限制條件相對較少,所以可以將半羣廣泛應用到軟件開發領域。
上面我們提及的最基本的G1(值-地址置換、地址-值置換、賦值置換)所具有的完備性,因此可以使用此置換來完整描述所有的基本功能。如果映射到實現中可以使用不同的方式來進行表示,而在實現中,爲什麼通過整數作爲基本的表達形式呢?
因爲,整數在數中是最爲簡單的數,所以整數完成的操作可以最爲簡單,所需的成本最小,同時整數在(加操作和乘操作上)具有環的特徵,但是在對於減操作卻不具有此特徵,因此,又引入了補碼的編碼方式,由此滿足了其數操作的完整性。
格:
格是一種特殊的偏序集,對其中任意兩個元素都可取最小上界(∨)和最大下界(∧)
設L是格,a,b,c∈L,則:
交換律:a∨b = b∨a , a∧b = b∧a
結合律:(a∨b)∨c = a∨(b∨c) , (a∧b)∧c = a∧(b∧c)
冪等律:a∨a = a , a∧a = a
如果針對具有菱形繼承關係是否是一個格呢?通過其定義我們可以看到,其具有同一個最抽象的父類(上界),和同一個所有繼承的子類(下界),其滿足上面提到的三個定律,所以其爲一個格,如圖2-7所示,都具有格的特徵。
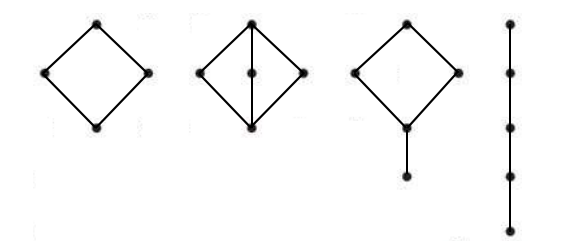
圖2-7


