遞歸介紹
遞歸:就是函數自己調用自己。 子問題須與原始問題爲同樣的事,或者更爲簡單;
遞歸通常可以簡單的處理子問題,但是不一定是最好的。
對於遞歸要分清以下概念:
- 自己調用自己
- 遞歸通常
不在意具體操作,只關心初始條件和上下層的變化關係。 - 遞歸函數
需要有臨界停止點,即遞歸不能無限制的執行下去。通常這個點爲必須經過的一個數。 - 遞歸通常能被其他方案替代(棧、數組正向求)。
認識遞歸,遞歸函數通常簡易但是對於初學者可能很難取理解它。拿一個遞歸函數來說。
static void digui()
{
System.out.println("bigsai前");
digui();
System.out.println("bigsai後");
}是一個遞歸吧?不是正常遞歸,沒有結束條件,自己一致調用自己死循環。
那正確的遞歸應該這樣
static void digui(int time)
{
if(time==0) {}//time==0不執行
else {
System.out.println("bigsai前time: "+time);
digui(time-1);
System.out.println("bigsai後time: "+time);
}
}對於這樣一種遞歸,它的執行流程大致是這樣的
所以,調用dugui(5)在控制檯輸出是這樣的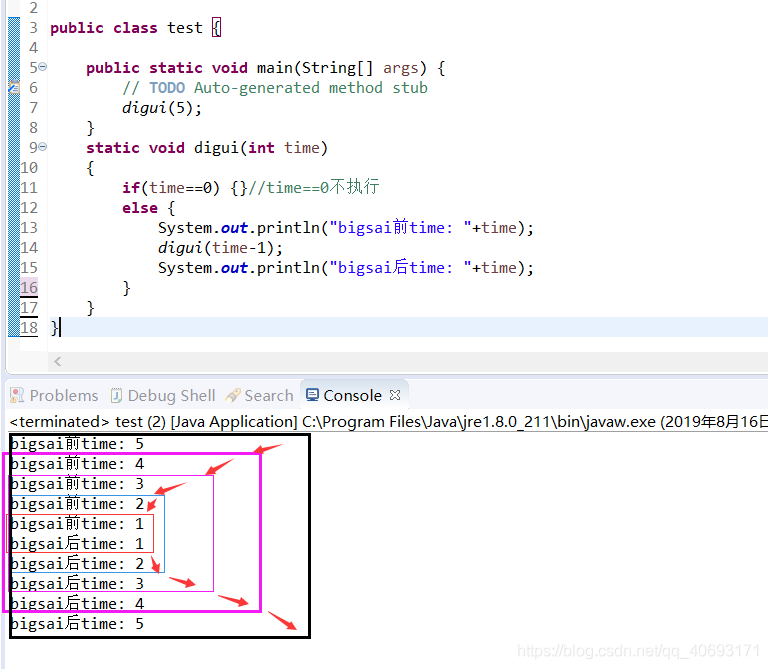
那麼,我想你對遞歸函數執行的流程應該有所瞭解了吧。
遞歸求階乘
求 n!=n*(n-1)*-----*1=n!=n*(n-1)
所以階乘的上下級的關係很容易找到。我們假設一個函數jiecheng(n)爲求階乘的函數。
這個階乘,你可以這樣命名:
int jiecheng(int n)
{
int va=1;
for(int i=n;i>0;i--)
{
va*=i;
}
return i;
}但是你還可以簡便這樣:
static int jiecheng(int n)
{
if(n==0)//0的階乘爲1
{
return 1;
}
else {
return n*jiecheng(n-1);//return n*(n-1)*jiecheng(n-2)=-------
}
}運行流程爲這樣:
遞歸求斐波那契
按照上述思想,我們假設求斐波那契設成F(n);
首先,斐波那契的公式爲:
F[n]=F[n-1]+F[n-2](n>=3,F[1]=1,F[2]=1)- 也就是除了n=1和2特殊以外,其他均是可以使用遞推式。
那麼遞推實現的代碼爲:
static long F(int n)
{
if(n==1||n==2) {return 1;}
else {
return F(n-1)+F(n-2);
}
}其實它的調用流程爲:
當然,其效率雖然不高,可以打表優化,後面可能還會介紹矩陣快速冪優化!
遞歸解決漢諾塔
漢諾塔是經典遞歸問題:
相傳在古印度聖廟中,有一種被稱爲漢諾塔(Hanoi)的遊戲。該遊戲是在一塊銅板裝置上,有三根杆(編號A、B、C),在A杆自下而上、由大到小按順序放置64個金盤(如下圖)。遊戲的目標:把A杆上的金盤全部移到C杆上,並仍保持原有順序疊好。操作規則:每次只能移動一個盤子,並且在移動過程中三根杆上都始終保持大盤在下,小盤在上,操作過程中盤子可以置於A、B、C任一杆上。
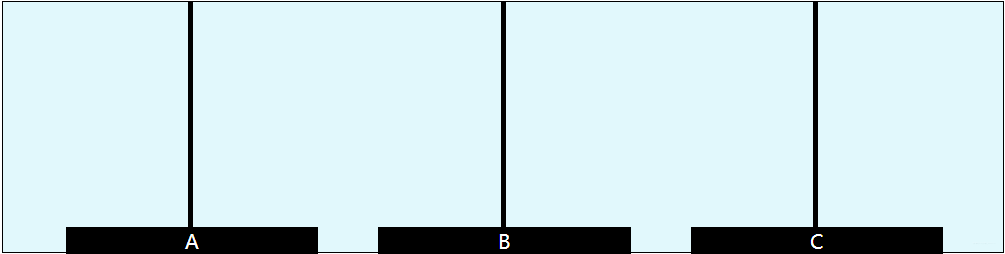
- 如果A只有一個(A->C)
- 如果A有兩個(A->B),(A->C),(B->C)
- 如果A有三個(A->C),(A->B),(C->B),(A->C),(B->A),(B->C),(A->C).
- 如果更多,那麼將會爆炸式增長。
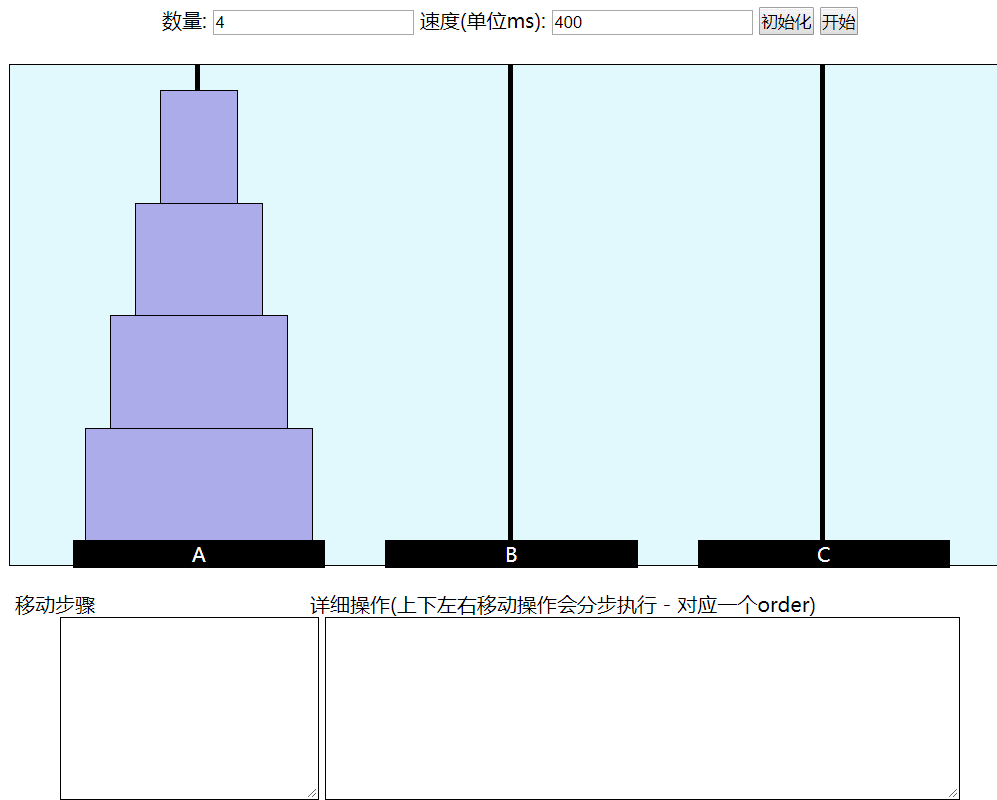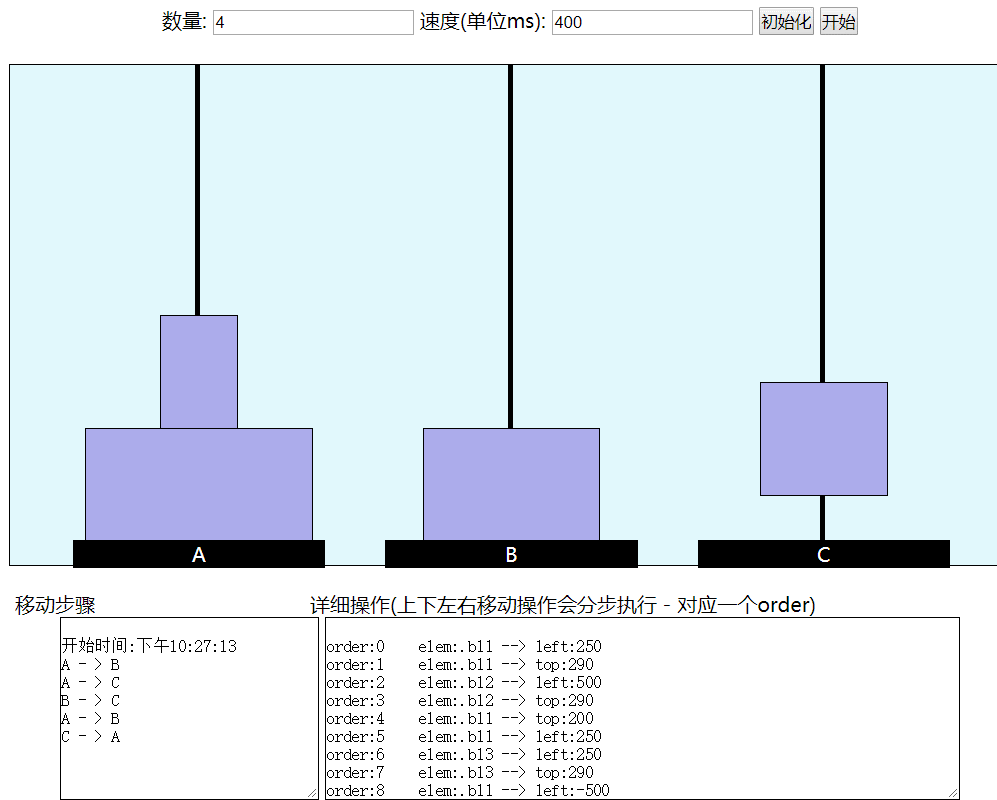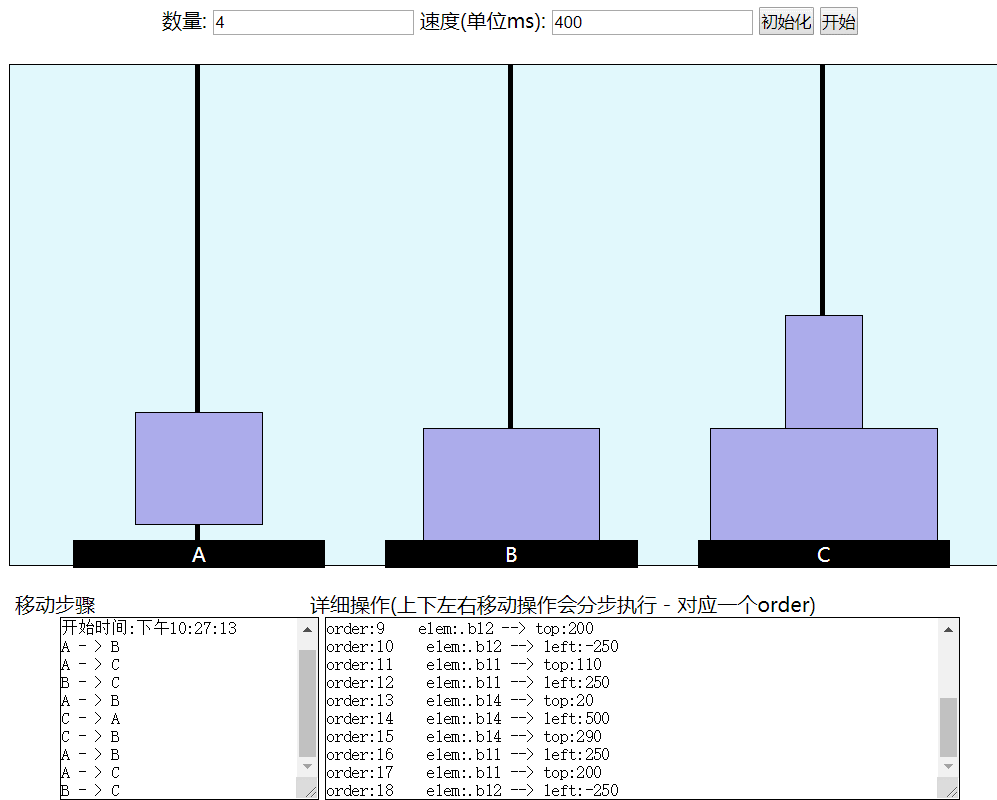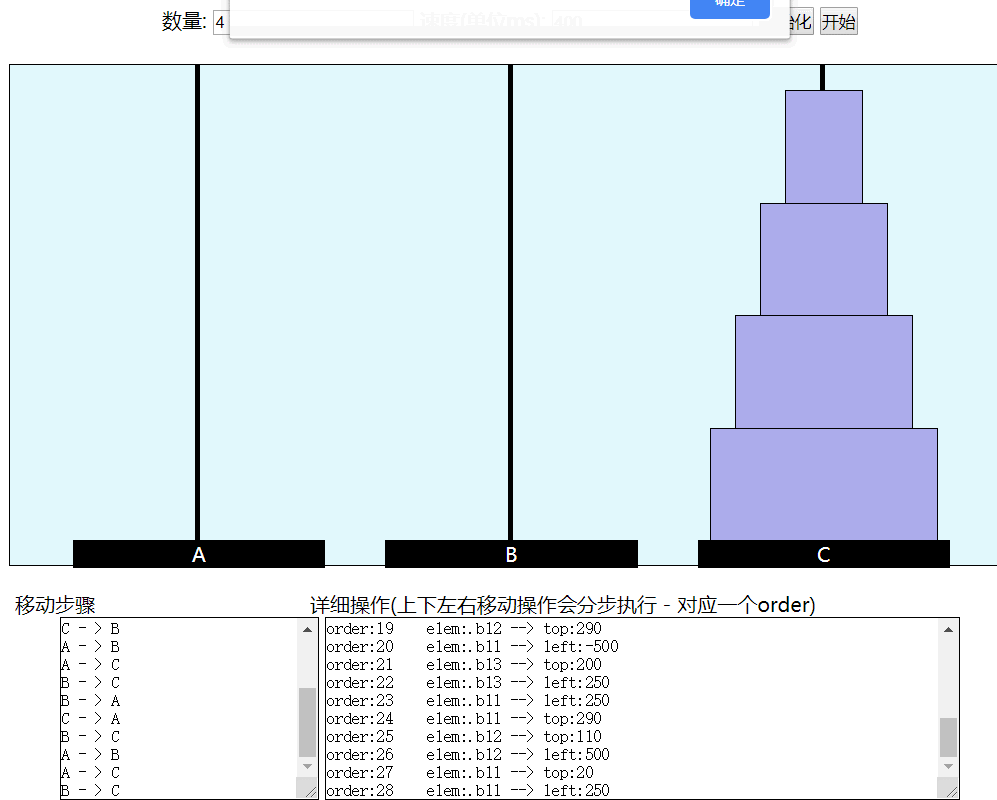
可以發現每增加一步,其中的步驟會多很多。但是不妨這樣想:
- 當有1個要從A->C時,且已知移動方式。使用函數表示move(a->c)。同理其他move操作。
- -------
省略中間若干步驟不看,用遞歸思想看問題
分析:n個從a—>c和n-1個a—>c有什麼聯繫?(hannuo(n)—>hannuo(n-1)有啥關係)
假設有n個盤子
- hannuo(n-1)之後n-1個盤子從A—>C.
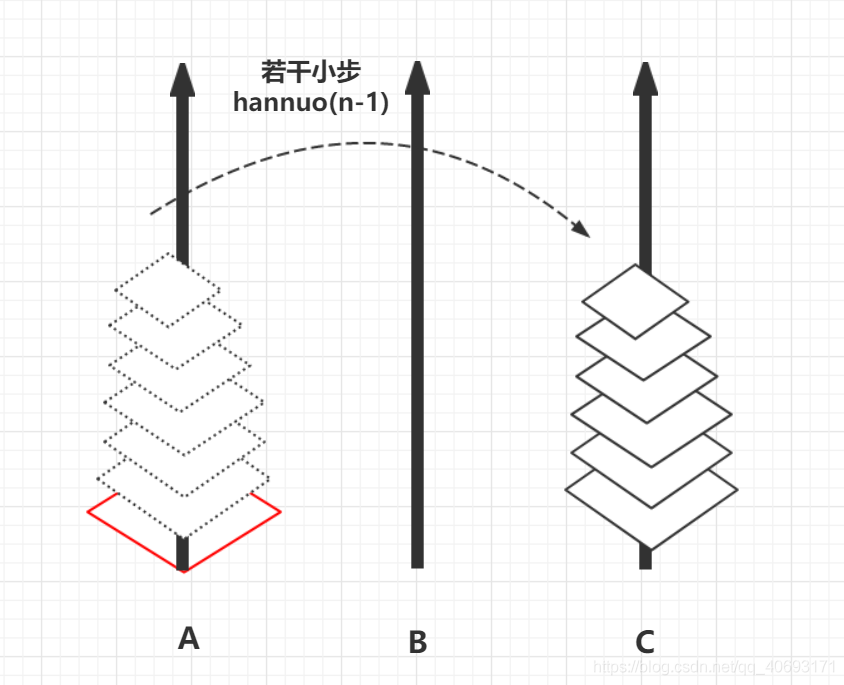
- 此時剩下底下最大的,只能移動到B,
move(A,B)
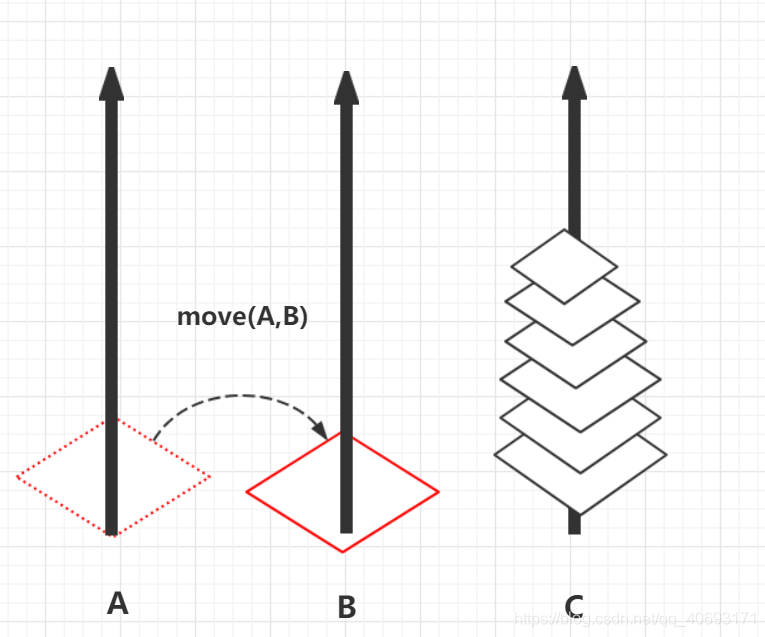
- 那麼你是否發現什麼眉目了,只需原先的huannuo(n-1)相同操作從C—>B即可完成轉移到B;那麼我們的之前函數應該寫成
hannuo(n-1,A,C)但是又用到B,所以把B傳進來hannuo(n-1,A,B,C)先表示爲從n-1個從A(藉助B執行若干操作)轉到C。
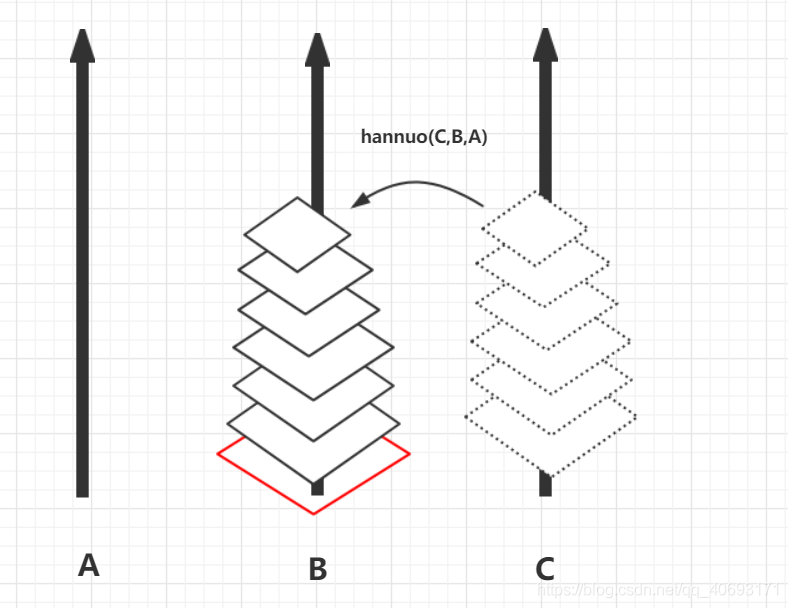
- 這一系列操作使得將n個盤子從A—>B但是我們要的是A—>C纔是需要的hannuo(n,A,B,C);那麼我們只需要
更改下hannuo(n-1,----)順序就好啦!
經過上面分析,那麼完整的操作爲:
package 遞歸;
public class hannuota {
static void move(char a,char b)
{
System.out.println("移動最上層的"+ a+ "到"+ b+ "\t");
}
static void hannuota(int n,char a,char b,char c)//主要分析每一大步對於下一步需要走的。
{
if(n==1) {move(a,c);}//從a移到c
else
{
hannuota(n-1,a,c,b);//將n-1個從a藉助c移到b
move(a,c); //將第n(最後一個)從a移到c。
hannuota(n-1,b,a,c);//再將n-1個從b藉助a移到c
}
}
public static void main(String[] args)
{
hannuota(5,'a','b','c');
}
}總結
其實遞歸在某些場景的效率是很低下的。尤其是斐波那契.從圖你就可以發現一個簡單的操作有多次重複。因爲它的遞歸調用倆個自己.那麼它的遞歸的膨脹率是指數級別的,重複了大量相同計算。當然這種問題也有優化方案的:
- 從前往後打表計算,採用類似動態規劃的思想。從前往後考慮。比如斐波那契F[n]=F[n-1]+F[n-2];那麼我
用數組儲存。從第三項開始F[3]=F[2]+F[1](均已知),再F[4]=F[3]+F[2]-----這樣,時間複雜度是O(N),線性的。 - 當然,對於階乘那種遞歸雖然
時間是沒有減少,但是如果需要多次訪問一個階乘,那麼可以採用同樣思想(打表)解決問題。
最後,筆者能力有限,如果有描述不恰當還請指正,感謝前面動態圖(未找到原作者)和漢諾塔動圖開源作者isea533的開源作品。同時,如果有喜歡學習交流的歡迎關注筆者公衆號:bigsai 回覆數據結構贈送精美資料一份!


