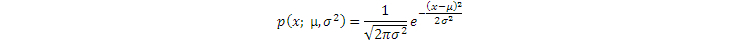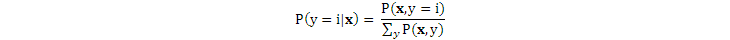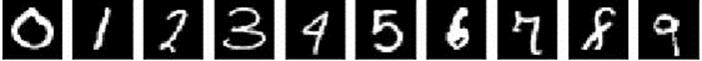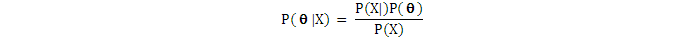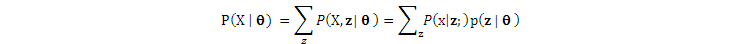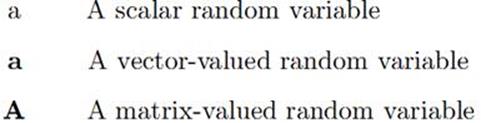第1章 概率分佈的模型表達及建模
1.1 模型
模型有很寬泛的定義,在Wikipedia上對Model的解釋裏就列出了多種模型及其定義。在我們要討論的內容的語義下,模型就是輸入與輸出之間關係的一種表達與實現。我們不關心模型內部對輸入量進行了什麼樣的操作而產生了輸出量,我們只關心輸入量與輸出量之間的關係或者說變化規律。模型與系統有大致相同的意義。
由於這種關係或變化規律有些可以用數學公式來描述,因而有的人會把模型當作函數。比如輸入量是x,輸出量是y,模型完成的功能用f來表示,我們有y=f(x)。但其實模型不是函數。
函數中的x和y之間的關係是確定的,或者說是靜態的。而模型表達的關係則是動態的,甚至是不確定的。比如在某個時刻輸入一個x並得到y,但換一個時刻輸入同樣的x,得到的卻是另一個y。用數學來描述就是,y(t) = f{x(t)}。注意,與一般的函數不同,這個模型的輸出也是時間的函數。而且,在非因果模型或系統中,輸出不僅與當前的輸入有關,而且還和過去甚至未來的輸入有關。這樣的例子有大家熟悉的卷積神經元網絡CNN,它也是一個模型或系統而不是函數:這裏,變化的不是時間而是空間,如果用不同大小的kernels對同一幅輸入圖像做卷積操作,你會得到不同的輸出結果。用數學來描述,就是y(s) = f{x(s)},s代表kernel的大小(假設 stride和padding的設置是不變的)。當然也可以說,函數表達了一個靜態的確定性的模型,是一般模型的一個特例。
1.2 概率分佈的模型表達
那麼,模型怎麼和概率有關係呢?這是因爲現實生活中我們遇到的概率問題大多涉及數量很大的隨機變量,很難用數學公式來描述它們之間的變化關係,但我們可以用概率模型來描述它們。
當然,我們已經有很多公式來描述多種多樣的連續隨機變量的概率密度分佈和來說隨機變量的概率,比如我們常用的高斯分佈。這些可以用公式來描述的概率分佈稱爲parametric distributions(參數型分佈),即這些分佈密度的函數具有固定的數學形式,其具體的函數值則取決於這些數學形式使用的參數。比如連續單變量高斯分佈:
其中,x是隨機變量,和是分佈參數,分別代表均值和方差,x的概率分佈p(x)的值取決於參數和。不同的參數決定了不同的概率分佈,但這些分佈的形式是一樣的。
如果一個概率分佈用參數型的公式來描述,那麼我們也稱這些分佈具有closed form(閉式)的表達。如果你知道一個隨機變量的概率分佈類型(比如高斯型),那麼就太好了,因爲你只要再想辦法確定這個分佈的參數值,就完全得到該隨機變量的分佈了。確定一個模型或系統的隨機變量分佈參數的通常辦法是,先由這個模型產生一些樣本{xi}, i=1..N,我們假設這些樣本來自概率分佈p(x),再通過極大似然法(maximum likelihood,簡稱 ML)或極大後驗概率法(maximum a posteriori, 簡稱MAP) ,尋找使這些樣本最可能出現的參數值。這是後面的核心內容之一。
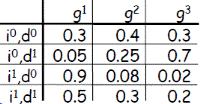
但如果我們無法用公式來描述隨機變量的概率分佈呢?有沒有別的辦法來描述?答案是:有,而且不只一種。比如,用表格的方式就可以描述離散隨機變量的概率。舉例來說,三個離散隨機變量I, D, G,分別取值{i0, i1}、{d0, d1}和{g0, g1, g2}。那麼條件概率P(G|I, D)可以用以下表格表示:
進而我們還可以進行一些inference(推理),比如求P(G|I)。這種表格形式的概率表達稱爲Table CPD (CPD=conditional probability distribution)。
注:簡單地說,"inference"指的是計算條件概率,即在觀察到某些隨機變量的取值時,計算其它變量的各個取值的概率或它們的聯合概率。我把它翻譯成"推理"。
同時,我們可以用圖的方式來表達多隨機變量之間的依賴關係。比如:
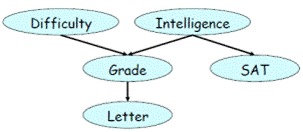
圖1. 貝葉斯網絡
這個圖裏的每個節點代表了一個隨機變量,節點之間的有向連線代表了變量之間的直接的依賴關係。比如,Grade(G)的概率受Difficulty (D)和Intelligence (I) 的影響,它的概率是P(G) = P(G|D, I)。括號裏的豎線表示條件概率。
這種用圖表達隨機變量之間的依賴關係的模型,稱爲概率圖模型 (Probabilistic Graphical Model,簡稱PGM)。其實更準確的叫法是概率的圖模型。
上圖是有向無環路的圖,隨機變量(即圖的節點)之間有明確的依賴關係,可以表達條件概率,因而稱爲貝葉斯網絡(Bayesian Networks),有時也稱爲信任網絡 (Belief Networks) 或條件隨機場(Conditional Random Field,CRF)。Belief Networks可能來自在概率圖上進行inference時(比如已知圖上各節點的概率,求所有的節點的聯合概率)所使用的信任傳播方法(Belief Propagation)。
並非所有的情形都能用貝葉斯網絡來表達。在有些情形裏,隨機變量之間的依賴關係並沒有明顯的方向,或者它們的依賴關係是雙向的,這時我們使用無向圖來表示它們的關係。無向圖(可以有環路)稱爲馬爾可夫網絡(Markov Networks)或馬爾可夫隨機場(Markov Random Felds MRFs)。
這種用圖的方式表達隨機變量之間複雜的關係的前提假設是,這些隨機變量之間的交互關係或相互影響是有所謂的"結構"的(簡單的關係比如父-子、上-下或前-後),這種結構就可以用圖的方式表達出來,這個圖也就等於爲這些隨機變量所構成的系統建立了模型,即圖模型。因此,圖模型也稱爲結構化的概率模型(Structured Probabilistic Models)。我們可以依據這個圖模型進行inference(推理)和採樣。
舉例來說,如果我們用鏈式法則展開5個隨機變量的聯合概率:
P(D, I, G, S, L) = P(I) P(D|I) P(G|D, I) P(S|D, I, G) P(L|D, I, G, S)
而圖模型具有一個重要優勢,就是在圖模型上進行推理或採樣時,所需的時間和存儲量更有可能是"tractable"(易駕馭的),這是因爲圖模型具有的隨機變量之間的結構信息被加以利用了,這大大減少了參與計算的參數的數量。比如上例,
P(D, I, G, S, L) = P(I) P(D) P(G|D, I) P(S|I) P(L|G)
可見,聯合概率的計算大大簡化了。
而其它非結構化的模型在解決這些問題時非常有可能是"intractable"(不容易駕馭的),即所需時間和存儲量按隨機變量的數量或取值空間大小的指數增長,因爲它們假設所有變量之間都有直接的關係。當然,還有些類型的模型走向另一個極端,即對隨機變量之間的獨立性做了過多的假設來簡化計算,但結果可能有較大的誤差。
再舉個概率圖模型的例子,這是在機器學習裏經常遇到的一類模型,叫plate model,用來表達重複出現的隨機結果。它與我們後面的討論有密切的關係。見圖2。
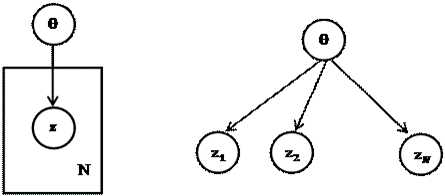
圖2左圖是plate model,方框就是plate,可以重複N次,裏面的圓圈代表隨機變量z的一次採樣結果,該結果出現的概率分佈取決於參數,參數的值不隨時間而變化,爲所有的plates共享,所以它在方框外面。右圖是左圖展開後的表現形式。
圖2. Plate Model
如果隨機變量是連續的呢?變量之間的依賴關係固然可以用PGM來表達,但概率分佈的密度就不方便使用Table CPD了(並非絕對不行)。如果也沒有closed form的表達,那麼我們就要想象有一個模型,你給它一個輸入(隨機變量的某個取值或採樣條件),它就給你一個輸出(概率值或者新的樣本),比如人工神經元網絡就是一個模型。現在我們要討論的是建一個概率模型(probabilistic model),它能準確地"捕捉"輸入的樣本之間的依賴關係及樣本的分佈,甚至可以自主"學習"不同類別的樣本所具有的抽象的"特徵",並可以產生符合樣本分佈的新樣本。
1.3 生成式模型(Generative Model)和判別式模型(Discriminative Model)
我們有兩類模型可以選擇。一類是Generative Model(成生式模型),另一類是Discriminative Model(判別式模型)。
簡單地說,生成式模型描述的是聯合概率P(x1, x2, …, xn, y),其中, x1, x2, …, xn, y都是隨機變量,就這個意義來說,xi和y沒有差別(y也可以由xn+1代替)。舉例來說,x=(x1, x2, …, xn)代表觀察值或者特徵值(features),比如一個人的血壓、血糖等各項體檢得到的生理特徵指標,y代表是否有某種疾病(y=1代表有, y=0代表沒有)。那麼 P(x1, x2, …, xn, y=1)表示具有那些生理指標和有病同時出現的概率,而P(x1, x2, …, xn, y=0) 表示具有那些生理指標但沒有病同時出現的概率。
有了這個模型P,我們還可以用它生成新的樣本(x1, x2, …, xn, y)。至於具體如何生成,後面會看到。
本文要講的VAE就是一種生成式模型。
而判別式模型用於描述條件概率P(y| x1, x2, …, xn)。就是說,如果我們知道x=( x1, x2, …, xn)的取值,我們可以根據這個條件概率通過這個模型獲得y的各個有效取值的概率。比如上例,P ( y=1 | x1, x2, …, xn)表示當那些生理指標具有觀察到的值的時候有病的概率。根據不同的x=( x1, x2, …, xn)值,通過這個模型可以判別哪些人可能有這種疾病,哪些人可能沒有。
如果y是連續的,判別式模型可以根據輸入對輸出做預測。
判別式模型無法生成新的樣本,因爲它不知道哪些(x1, x2, …, xn)的取值會最可能出現,即缺少P(x1, x2, …, xn)。它只能根據觀察到的(x1, x2, …, xn)值被動地對y的取值做判斷。從貝葉斯公式出發,我們有
P(x1, x2, …, xn, y) = P ( y | x1, x2, …, xn)P(x1, x2, …, xn)
所以只有P ( y | x1, x2, …, xn)是無法生成新樣本(x1, x2, …, xn, y)的,還需要知道P(x1, x2, …, xn)。
生成式模型也可以用於分類,即在y的不同取值時,哪個取值得到的聯合概率大,就認爲y屬於哪個分類。所以,生成式模型獲得了每個分類的分佈,然後再判斷一個新樣本最可能屬於哪個分類:
而判別式模型獲得的是各個類之間的邊界。有個比喻是,生成式模型學會所有的語言才能判斷某個人說的是哪種語言,而判別式模型不學習任何語言,而只是知道不同語言之間的差別就能判斷某個人說的是哪種語言。一般認爲,生成式模型未必能準確獲取隨機變量之間的關聯,而判別式模型則不要求知道這種關聯(它根據的是全部特徵值對y產生的共同作用),所以,在做分類時,判別式模型的性能比生成式模型要好一些。當然,這也要看具體的情況。
我們根據要解決的問題,確定選擇什麼類型的模型。
1.4 一個生成式模型的實例
再舉個例子吧。假如我們有類似以下手寫體數字的樣本:
在數據集MNIST裏,這樣的樣本有六萬個,都是不同的人寫的,風格各異,但我們還是能準確認出絕大部分,準確率在99%以上。
我們希望用MNIST樣本集建一個模型,它可以產生新的手寫體數字,這些數字雖然很像樣本集裏的那些數字,但仔細看卻不完全一樣。或者說,新產生的數字沒有一個是和原樣本集裏的一模一樣,但仍然很相像。
這就是生成式模型要解決的問題。
假設已知數據集X裏有 N個樣本(樣本也稱爲數據點):
x = {x(i)}, i=1..N,
其中,x是一個隨機變量,x(i)是隨機變量x的第i個樣本。x可能是多維的,各個維度的取值可以是連續的,也可以是離散的,但必須一致。
比如MNIST樣本集,每個樣本是一幅28x28大小的圖像,因此,x是一個28x28=784維的整數向量。圖上每個像素可以有256級灰度值,因此x是離散的隨機變量。x 的取值空間巨大,有25628x28個取值可能。如果我們用x={"0"}表示784個像素的取值呈現出 "0"的圖像的那些x的集合,那麼由於每個人寫字的風格不同,這個集合裏的元素肯定不止一個。
這些樣本的獲取或採集過程符合一個所謂i.i.d.的條件,即 independent and identically distributed (i.i.d.)。就是說,每個樣本都是獨立地採集的,彼此沒有影響;而且,每個數字的樣本數大致相同。比如MNIST裏的各個數字的樣本數是:
{0: 5923, 1: 6742, 2: 5958, 3: 6131, 4: 5842, 5: 5421, 6: 5918, 7: 6265, 8: 5851, 9: 5949}
i.i.d.是一個非常重要的條件,許多概率論和機器學習裏面的理論推導都要用這個條件。在很多情況下,爲了簡化解決問題的過程。我們也經常假設這個條件是成立的。但如果這個假設是錯誤的,那麼我們得到的問題的解就有誤差。
對於MNIST樣本來說,一個784維的向量的取值不是任意的。這784個像素的取值一定要構成一個我們認得出的數字的圖形,它纔在樣本集裏。任意取值而構成的圖形很可能就是一幅完全沒有意義的圖。或者說,那些手寫數字的人們在寫這些數字時,必須遵循每個數字的特定的筆劃結構,遵循這樣的結構寫數字,就是遵循一定的規律給這些像素賦值。這個規律,就是我們要追尋的統計規律Pgt(X),代表probability,gt代表ground truth。爲什麼用統計規律而不是筆劃的結構規律呢?因爲前者更通用,而且更容易用數學來表達和建模。
假如我們用x= "8"代表一個樣本的784個像素的取值構成數字8的圖像。爲了討論方便,我們假設每個像素的灰度值只有0和1。顯然,不同的人寫出來的 "8"具有不同的風格。但如果你想像一下這些 "8"的圖像在784個像素位置的灰度值,你會得出結論,那就是,不同的樣本,灰度爲1和爲0的像素位置即使不完全一樣也大致差不多。比如手寫數字的傾斜度不同的兩個樣本上,灰度值爲1的彼此對應的點雖然不在同一個像素位置,但它們在相鄰的像素位置;或者也許灰度值爲1的像素在一些樣本上比另一些樣本上要多一些(筆畫較粗)。但這些不同都不會改變它們具有"8"的結構。每個像素取值1還是0並不是任意的,而是有一定的概率,比如落在"8"的筆畫上或附近的像素,取1值的概率遠大於取0值的概率。如果樣本確實來自分佈Pgt(X),那麼 Pgt(x="8")告訴我們,只有當784個像素點的灰度值呈現了"8"的結構,這個概率才具有非常大的值,否則就有非常小的值。如果我們只看"8"的樣本,那麼它們在784維空間裏的取值符合高斯分佈,這時它是一個條件概率分佈,即P(x|z="8"),z是樣本的分類,代表數字"0"到"9"。而全體樣本的Pgt(X)則像在784維空間裏的K-Means或者GMM的結果,它把樣本點聚集在10個集羣裏。
但是,我們幾乎沒有辦法找到Pgt(X),雖然我們知道它是真實存在的。這就如同我們用機器學習算法去找一條擬合樣本點的方程h(X)一樣,我們無法知道h(X)就是實際產生那些樣本點的方程g(X)。所以我們退一步,希望利用那些樣本構建一個模型,該模型經過訓練,能夠學習到樣本里蘊含的統計規律P(X),使得P(X)非常接近Pgt(X)。
可見,我們通過樣本要構建的模型P(X)是一個概率模型。其實,因爲我們希望能用這個模型產生無數多個"0"到"9"的不同的手寫體新樣本,我們也不需要這個模型實現的是一個確定性的函數(即使有這種可能)。
建立好的模型(具有確定的模型結構和訓練好的模型參數),除了可以產生新的樣本外,我們還可以用它來做推理(inference),即根據觀察到的一些隨機變量的取值,推理出另一些隨機變量出現不同取值的概率,這涵蓋分類,去噪音,修補殘缺的圖等應用。
1.5 建模的思路
一般來說,我們首先建一個模型的結構,比如深度學習網絡。初始時,這個模型輸出的數據的分佈肯定離我們的目標分佈相差很遠。同時,我們有大量的樣本,並且相信,這些樣本來自一個未知但真實的概率分佈Pgt。然後,模型結構利用這些樣本不斷修改自身的參數(即學習的過程,比如依據最大似然原則,使用梯度下降法),使其輸出數據的分佈越來越接近數據樣本的分佈。當二者足夠接近時,我們就獲得了所需的模型,它包含模型的結構和模型的參數。
同樣的模型結構使用不同的訓練方式,我們會獲得不同類型的模型。通常,生成式模型的訓練是Unsupervised Learning(其實是self-supervised learning),判別式模型的訓練是Supervised Learning。
我們要建的是概率模型(probabilistic models),而不是確定性的模型。這個模型的輸入輸出都可被視作是隨機變量。這個模型必須能準確"捕獲"這些數據樣本所具有的內在統計規律,即它的P(X)是真實的概率分佈Pgt(X) 的近似。我們的任務就是估算數據集的概率密度或概率分佈。
如果我們選取假想的P(X)是參數型的概率分佈,那麼,我們的目標是通過觀察到的樣本數據集X獲得樣本數據分佈的參數集。注意,是可能包含多個參數的向量,而且每個參數可能是多維的。
我們從貝葉斯公式出發:
其中:
P()是分佈參數的prior(先驗概率)。這是一開始我們要做的假設,或者說在觀察到任何數據前,我們相信符合分佈P()。數據集X會在P()之上不斷調整的分佈,直至它足夠接近真正的分佈,即後驗概率分佈。
P(X|)是likelihood(似然概率),即在當前參數下,出現我們觀察到的數據X的概率。如果數據集X裏有多個樣本,我們假設它們都是i.i.d.的,這樣當我們計算似然概率時,可以單獨計算每個樣本出現的似然概率,再把它們相乘(取log-likelihood時就是相加)。
注意,如果是固定的而X是隨機變量,則P(X|)是X的採樣(sampling)。
有的文獻使用marginal likelihood一詞,它與P(X|)差不多,但是增加一個latent variable(隱藏變量)向量z,再把z"邊緣化"(即marginalized或在z爲離散量時被sum-out):
至於爲什麼引入latent variables,我們後面再解釋。
P(X)是evidence(證據)、即我們觀察到的數據集X出現的概率。
P(|X)是posterior (後驗概率),是我們的目標,即在觀察到數據X後,分佈參數應該調整到什麼值。此即新的分佈參數。爲了與當前參數區分開,我們給加上下標:New 和Current 。
在此規範一下本文使用的一些術語和記法:(來自http://www.deeplearningbook.org/contents/notation.html)。
如果是確定性的未知量,如圖2中的,我們把它稱爲參數,則似然概率分佈記爲P(X ; ),意思是數據X是由參數爲的分佈產生的。由於P(X; )是的函數,故一般稱它爲似然函數;如果參數被當作未知隨機變量的一部分(貝葉斯的哲學是所有未知量都是隨機變量,所以也有概率分佈),則把似然概率分佈記爲P(X|)。
對於參數,我們可以估計其實際值,即從非完整、非確定且有噪音的數據X中計算出X的近似分佈參數。而對於隨機變量,我們使用推理(inference)來計算它的分佈,即用X的觀察值和先驗證據推導出後驗概率P(|X)的過程。前者計算出參數的本身,後者推導出參數的分佈(把當作隨機變量)。
目前,尋找數據集的分佈參數或其後驗概率的途徑有兩個,一是採樣法,比如MCMC;另一個是使用類似最大似然法的優化法,獲得近似解。後一個途徑又有兩個常用的算法,一是Expectation-Maximization (EM) 算法,另一個是與本文的重點密切相關的Variational Inference (VI) 算法,有時也叫Variational Bayesian Inference(VB)。我們一一介紹。
下一章先對MCMC用於Bayesian Inference做個簡要介紹。