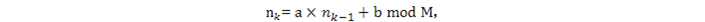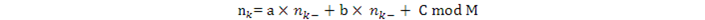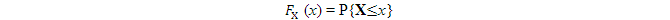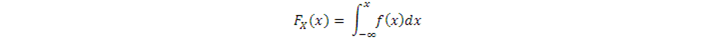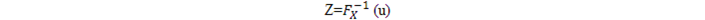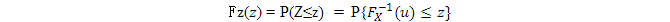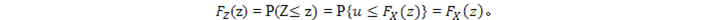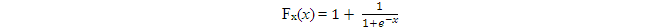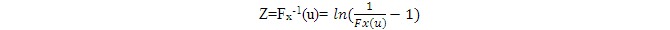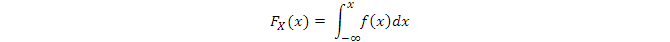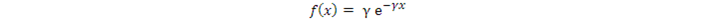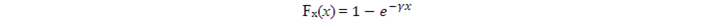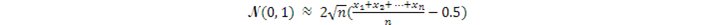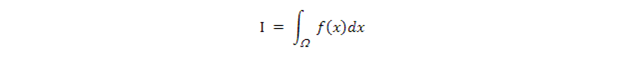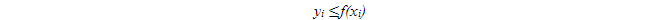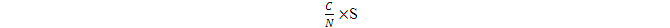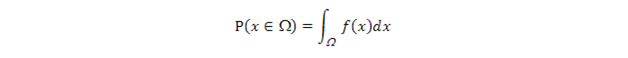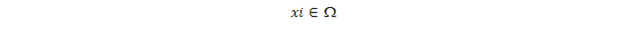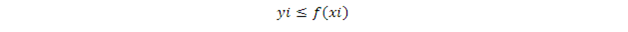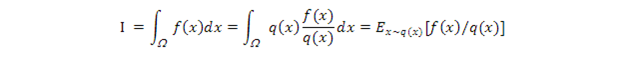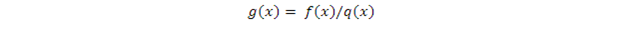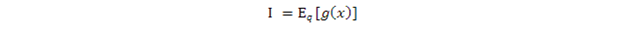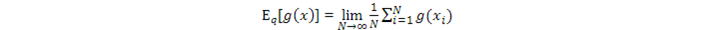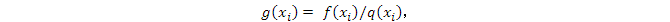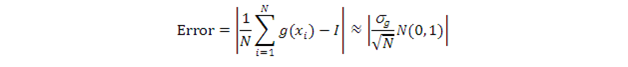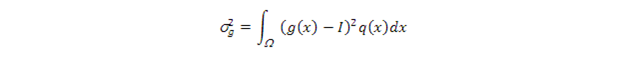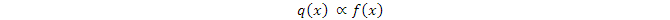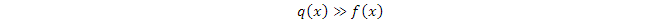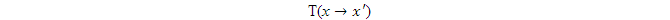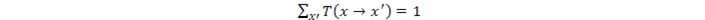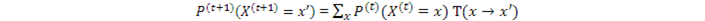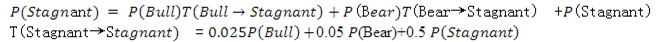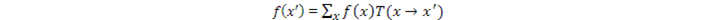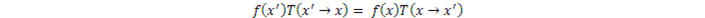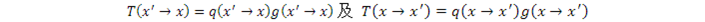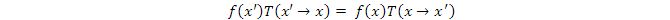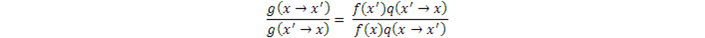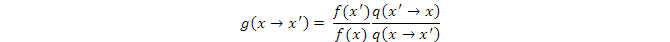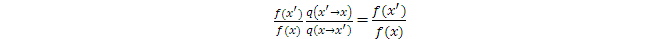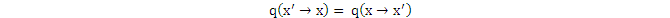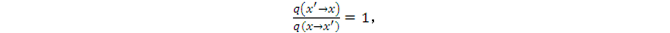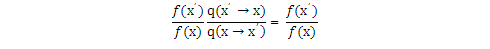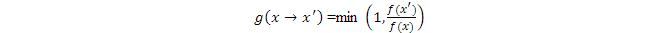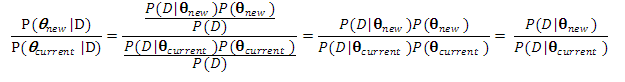第2章 分佈密度估算的採樣法
2.1 如何採樣
有了概率分佈P(X),我們要生成符合這個分佈的樣本。這個過程也叫採樣(sampling)。
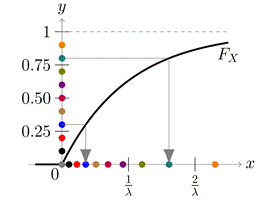
這其實並不是一個簡單的任務。我們知道,計算機可以生成符合某些指定分佈的僞隨機數(僞隨機數即樣本),但並不支持任意的分佈。對於所支持的非均勻分佈的僞隨機數x的產生,我們需要先產生均勻分佈的僞隨機數y,然後通過某種變換,把y轉換成指定的非均勻分佈的x。例如下圖,y軸上是一些均勻分佈的點,通過某個函數Fx映射到x軸,就得到非均勻分佈的點了。如果函數Fx足夠複雜,我們可以把任意一個分佈轉換成另一個分佈。如何在兩個分佈之間找到這樣的函數,這是VAE的關鍵點之一。
均勻分佈的僞隨機數的生成常用兩個算法,它們都是用數列迭代的方法產生僞隨機數。一個叫線性同餘序列(Linear Congruential Generator, LCG),公式是
來自https://en.wikipedia.org/wiki/Inverse_transform_sampling
產生[0, M]之間的一個隨機數。a或b,以及M要足夠大纔能有好的結果。早期的Matlab使用的是這個算法:a=75,b=0, M=231 – 1。
n0是初始數,稱爲"種子"(seed)。若要重現實驗結果,在產生隨機數時要提供使用的seed。
另一個叫Lagged Fibonacci Generator,公式是
新版的Matlab (>R5.0) 使用的是這個算法 :a=1,b=1, =17,=5。
均勻分佈到非均勻分佈的轉換方法也有兩種,一種可以稱爲CDF Transformation,另一種可以稱爲PDF Transformation。
前者需要知道隨機變量的CDF(Cumulative Distribution Function),即離散變量
連續變量
先在均勻分佈上採集一個隨機變量u,則
就是符合Fx分佈的隨機變量,即Z具有與X相同的分佈。Fx-1是Fx的逆函數。
證明過程很簡單。Z的CDF是FZ(z),
大括號內的不等式兩邊加上FX,則左邊變成u,右邊變成FX(z)。CDF具有單調性,所以上面的不等式加上FX 也不改變不等號的方向。因此,
證畢。
顯然,只有當Fx-1有解析解時,CDF Transformation纔是可行的。
比如,
則
如果我們知道的是x的概率密度函數f(x),爲了使用上述方法,我們要先計算它的CDF:
這一步也無法保證有解析解。下面是一個有解析解的例子:
則
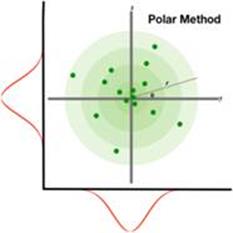
第二種方法是PDF Transformation,直接利用概率密度函數(PDF)推導出函數h,使得X = h(U)把均勻分佈的樣本U轉換成需要的X的分佈。這個方法避免求積分,但需要求h-1的雅可比矩陣,看上去也不是一個容易使用的方法。我們常用的標準高斯分佈(x) ~ N(0, 1)的僞隨機數的產生方法是Box-Muller公式,其推導就使用了PDF Transformation,但用了一個巧妙的方法,即極座標方法,避開了實際求雅可比矩陣,這裏就不展開了。下圖直觀地解釋了這種方法的原理:每個圈(從淺綠色到深綠色)裏的數據點的數量基本一樣(在極座標裏是均勻分佈的),但在x-y座標系裏就是高斯分佈的了(點的密集度從中央到邊緣越來越低,其實在x-軸和y-軸上的分佈都是高斯分佈)。
Polar method is sometimes more convenient to think of generating a pair of random variates (x, y) from the target distribution p(z). We can map this pair to a representation in polar form (rcosθ, rsinθ), which exposes other mechanisms for sampling, e.g., the famous Box-Muller transform is derived in this way.
來源:http://blog.shakirm.com/2015/10/machine-learning-trick-of-the-day-4-reparameterisation-tricks/
對於標準正態(高斯)分佈N(0, 1),另一種採樣方法是利用中心極限定理,從二值分佈(Bernoulli分佈)大量地採集樣本x1,x2,…,xn,然後計算出一個高斯隨機數:
問題是,這個方法需要很長的計算時間,因爲每個高斯隨機數的產生都要先產生n個Bernoulli分佈的隨機數。因此一般我們還是用Box-Muller公式,直接把均勻分佈轉換成標準高斯分佈。
至此,我們知道如何對一些常見的有公式表達的概率分佈進行採樣了。我們記住這些方法的思路,就是先得到均勻分佈的樣本,再通過一個函數把這些樣本轉換成所需的分佈的樣本。進一步延伸,我們應該可以把從已知分佈(不一定是均勻分佈)採樣的樣本,通過一個函數,轉換成我們需要的任意分佈。這裏,我們的任務就是找到這個函數。
2.2 蒙特卡羅方法
那麼,如果概率分佈f(x)是任意的,同時CDF Transformation和PDF Transformation都很難或無法找到解析解呢?這時我們一般使用一個直截了當的採樣方法,名爲MCMC(Markov Chain Monte Carlo)的採樣方法,中文翻譯成馬爾科夫鏈-蒙特卡羅方法,就是在馬爾科夫鏈上跑蒙特卡羅方法,所以它有兩個部分,即蒙特卡羅方法和馬爾科夫鏈。
先簡要介紹一下蒙特卡羅方法(這時你的頭腦中是否閃現過一個念頭:也許還有拉斯×××方法?)。這個方法的最初目的是求定積分:
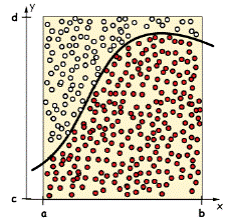
其中,是定積分的x取值域。這個積分問題的難處在於函數f(x)很複雜,或者x的維度很高,使得這個定積分沒有或很難找到解析解,常規的數值方法也不適用。這時我們可以用採樣的方法來求I的近似值。先看個x爲一維的簡單例子(下圖來自Wikipedia) :
我們來求的近似值。方法是在上圖的正方形裏撒均勻分佈的N個點(紅+藍),計算出落入1/4圓裏面有C個點(紅)。正方形的面積是1,則圓的面積是
4C/N = r2 =
f(x)
對單一的一維變量x的函數f(x)做定積分,就是求f(x)的曲線下的面積。無論f(x)的曲線多麼複雜,我們都可以把需要積分的這段放在一個正方形裏,再用上述方法計算曲線下的面積。假如正方形的面積是S,N個均勻採樣點{(xi, yi), i=1..N}中有C個點滿足
則f(x)下的面積約是
當N足夠大時,這個面積就近似於f(x)的定積分。這就是基本的蒙特卡羅方法。
這個方法需要在座標系的橫軸和縱軸方向以正方形爲界,採集均勻分佈的多對點{(xi, yi), i=1..N}。如果x是多維變量,那就需同時在各個維上採集均勻樣本點。均勻分佈的採樣我們在上面已經介紹了。
這種計算定積分的近似值的方法稱爲Rejection Sampling。意思是,N個採樣點中,只有落在f(x)曲線下的區域裏的C個樣本點才被接受(上圖中紅色的點),在這個區域之外的點(藍色的點)被拒絕。
那麼,定積分的這種近似解法和任意分佈f(x)的採樣有什麼關係 ?因爲CDF的計算公式是
我們可以用"拒絕"的方法把
內的均勻採樣得到的樣本點{(xi, yi), i=1..N}檢查一遍,只留下滿足
的那些xi點作爲符合f(x)分佈的樣本點,其它的點都被拒絕。這樣,在f(x)越大的地方,留下的樣本點越多,因爲這些地方的f(x)下的面積也大。最後留下的{xi}就是合法的樣本點。這也算是一種從均勻分佈到任意分佈的轉換方法。
這個方法的缺點是,如果那個正方形與f(x)之間的間隙比較大,比如當f(x)的曲線有 "陡峭的山峯"形狀,則被拒絕的採樣點也很多,造成較大的浪費(獲得這些採樣點所花的計算資源和時間)。
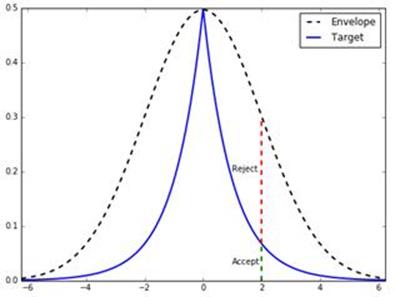
提高效率的一個方法是Importance Sampling,意思是,f(x)取值大的地方(即"尖銳的山峯"處)所取樣本的點數應該多於f(x)取值小的地方,即越重要的地方,樣本點應該越多,越密集。這也是概率密度的本意。下面是一個例子,來自http://bjlkeng.github.io/posts/markov-chain-monte-carlo-mcmc-and-the-metropolis-hastings-algorithm/。
圖中藍線的Target(即f(x))是雙伽馬分佈(Double Gamma Distribution)。可以看到,它有尖銳的"山峯"。如果我們圍繞它畫一個矩形(假如我們知道f(x)的峯值),並在這個矩形裏進行均勻採樣,那麼被拒絕的點會非常多(落入藍線條以上的區域的點)。但如果我們能用一個Envelope函數q(x)覆蓋f(x),然後在橫座標方向以q(x)爲分佈採樣xi,在縱座標方向繼續以均勻分佈採樣yi,那麼被拒絕的點就會少很多,因爲大多數xi被q(x)集中在中間"山峯"的位置。當然,q(x)的選擇是個關鍵,它必須滿足兩個特點,一是它足夠簡單,容易採樣,二是能大致符合f(x)的形狀,使q(x)和 f(x)之間的空隙儘可能地小。圖中,黑色虛線q(x)是高斯分佈N (0, 2)。在f(x)的取值大的區域,從q(x)生成的樣本xi也聚集得多。前面的內容已經講過如何從高斯分佈採樣(Box-Muller公式)。這樣,我們可以用一個簡短的程序就能實現雙伽馬分佈的Importance Sampling。
注意,來自q(x)的樣本xi被接受的概率等於f(xi)/q(xi),即f(xi)和q(xi)的高度之比。這是因爲在縱向的採樣是在0 ~ q(xi)之間的均勻採樣,樣本點落入f(xi)以下部分的概率是f(xi)/q(xi)。請仔細觀察圖中的綠虛線和紅虛線之間的關係。Importance Sampling也是一種Rejection Sampling,只不過在橫軸方向的採樣不再是均勻分佈的,而是按照q(x)的分佈採樣。
讓我們再用數學語言來描述一下Importance Sampling。
我們要求的積分
最後這個等號來自期望值E的定義。我們設
這樣上式簡記成
類似地,如果x是離散隨機變量,可以求得
這樣,我們把求積分(或求和)轉化爲求期望值。注意E的下標,它說明x的分佈必須符合q(x),或者說,x來自q(x)。那麼如何求期望值呢?
根據大數定理,如果我們通過q(x)採集大量的i.i.d.樣本xi,i =1..N,那麼我們可以用g(xi) 的均值近似g(x) 的期望值:
其中,
而f(x)和q(x)都是已知的,計算所有樣本點的g(xi)的均值就可以得到I的近似解。這就是Importance Sampling的數學表達。
上面的公式中,g(x) = f(x)/q(x)。前面說過,g(x)的意義是,它是來自q(x)的樣本x被接受的概率。
我們也可以解釋
的意義:xi 被選中的概率是q(xi),它被接受的概率是g(xi),那麼,xi 最終成爲合法的樣本點的概率f(x)是它被選中並被接受的概率,即這兩個概率的乘積q(xi)g(xi) 。
同時,大數定理還告訴我們,在N是有限值時,均值到期望值之間的誤差是:
其中,
此項即方差(variance);而N(0,1)是標準高斯分佈。
注:大數定理(Law of Large Numbers)的另一個名字是我們前面提到過的中心極限定理(Central Limit Theorem),前者可能在信息論裏較常使用,後者在概率論裏較常使用。
這個定理是概率論裏最本質、最核心的定理,但它的證明比較複雜,思路是先把多個隨機變量之和用其特徵函數變換一下(關於特徵函數,可參閱https://en.wikipedia.org/wiki/Normal_distribution裏面的相關內容),再用泰勒級數展開特徵函數,最後利用高斯函數的傅立葉變換就是其本身這個性質完成證明。這裏就不再進一步展開了。
顯然,當g(x) = I 時,誤差趨於0。此時,
此q(x)即全部符合條件的q(x)中的最佳q(x)函數,記爲q*(x)我們在前面說過,q(x)最好能大致符合f(x)的形狀,現在這句話得到了數學解釋 --- 這樣的q(x)會使方差儘量小,亦即使誤差儘量小。
如果能找到q*(x),則我們只需一個樣本(即N=1)就能得到誤差爲0的估計值。之所以如此,是因爲q*(x)已經解決了最初的求積分的問題,而這是無法做到的(所以才需要估值的方法)。既然q*(x)是無法得到的,我們就要專注找其它能使方差減小的q(x)。在後面講MCMC算法和Variational Inference算法時,我們還要回到找最佳q(x)這個話題。
q(x)對提高採樣效率具有重大影響,選的不好會使採樣效率變低。
從g(x)= f(x)/q(x)可以看出,如果q(x)產生的樣本使g(x)很大,則方差也很大,而這種情況會發生在當q(x)很小時。所以我們希望q(x)大一些。但另一方面,如果
則樣本的拒絕率會很高。所以q(x)也不能太大。總的來說,x的維數越高,好的q(x)越難找,近似算法的誤差也越大,爲減小誤差所需的樣本也越多。這裏從另一個角度揭示了x的維數與模型學習所需樣本數之間的關係。
即便找q(x)存在風險,但Importance Sampling讓我們以較高的效率採集符合已知概率分佈的樣本。而且,它利用大數定理,把求積分(或求和)轉換成求期望值,再轉換成求大量樣本的均值這個思想,在機器學習的很多算法,包括深度學習的很多算法中被廣泛使用,而且上面對q(x)的討論可以幫助讀者深刻理解VAE和其它生成式模型。
2.3 馬爾科夫鏈
在隨機變量的維數比較高的時候,好的q(x)是很難找到的,這時馬爾科夫鏈就出場了。
一個馬爾科夫鏈定義了一個狀態轉換模型
其中x和x' 表示狀態,x→x' 表示狀態x轉化到另一個狀態x' ,狀態轉換概率是T。所以,對所有的x,必須有
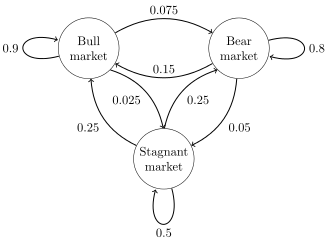
下面這個例子和圖來自Wikipedia,是一個股市預測模型。
這相當於有一個隨機變量market,它有三個取值,即用圓圈表示的三個狀態:x0='Bull market' ,x1='Bear market'和x2='Stagnant market'。而圓圈之間的有向連線表示狀態之間的轉換關係,旁邊標註的數字是該轉換的概率T。一個狀態可能保持不變,所以,一個圓圈到自己也有"狀態轉換"概率。
特別提醒一下,圓圈代表的不是隨機變量,而是隨機變量的狀態(即可能的取值)。如果一個模型裏包含多個隨機變量,或隨機變量是多維向量,那麼一個狀態就是這些變量或向量各維的某個聯合取值。
用X表示狀態,x表示狀態的取值,P表示某個狀態出現的概率,T表示狀態轉換概率,t表示時間步數(time step)。每個time step狀態轉換一次。則新狀態的概率更新爲:
比如上圖,
這就是說,當前時刻(t+1時)的狀態只由上一時刻(t時)的狀態所決定,與更早或更晚的狀態無關。這是馬爾科夫鏈的關鍵思想。
注:雖然這裏的定義和例子是針對離散隨機變量的,但也同樣適用於連續隨機變量,只不過求和變成求積分。以後不再特別說明。
在馬爾科夫鏈上,如果在有限的步數內,一個任意狀態到另一個任意狀態的轉換概率大於0,則稱這個馬爾科夫鏈是Regular Markov Chain,也叫各態歷經的馬爾科夫鏈。這種馬爾科夫鏈有個性質,就是狀態不斷地轉換,最終會進入一個唯一的穩態(stationary state),此時P(X)不再變化。我們用f(X)取代P(X)來表示穩態時的各個狀態出現的概率。如果T選擇得合適,那麼可以證明,f(X)正是我們要從中採樣的目標概率。此時繼續運行馬爾科夫鏈,即繼續進行狀態轉換,那麼,每個狀態出現的次數與它的概率f(X)成正比。也就是說,每次的狀態轉換相當於一次從f(X)的採樣。這就是MCMC的核心。
模型處於穩態時,滿足條件:
不過,我們會利用一個更強的稱爲Time Reversibility的條件:
即狀態從x' 轉換到x與從x 轉換到x' 具有相同的可能。這種狀態也稱爲Detailed Balance。要想使穩態時的各狀態的概率(或分佈)是我們希望的f(x),關鍵是找到合適的狀態轉換概率T。
2.4 MCMC的Metropolis-Hastings算法
如果我們任憑馬爾科夫鏈完全跟隨概率T更新狀態,那麼,在X的整個狀態空間中,從一個狀態轉換到相距較遠的另一個狀態可能是非常困難的,因爲狀態轉換都有本地化的傾向,即相鄰的狀態之間較容易轉換,結果是,出現相距當前狀態較遠的某些狀態很難出現,或者說,要經過大量的採樣纔會出現,無論它們的概率是什麼。因此,採樣的效率不高。解決辦法是,讓Importance Sampling運行在馬爾科夫鏈上。這就是MCMC的Metropolis-Hastings算法。我們將看到,這個算法一舉兩得,即解決了狀態轉換概率T的選擇問題,又解決了下一個狀態的選擇問題(即找好的q(x)的問題)。
Metropolis-Hastings算法的關鍵之處在於,它把狀態轉換概率T分解成兩部分:
其中,q是proposal概率(當x是連續的,q是分佈函數,下同),比如q(x→x' )表示以當前狀態x爲起點,建議跳到下一狀態x' 的概率,或者說x' 被選中成爲新狀態的概率。q的作用與Importance Sampling中的q(x)是一樣的;g是接受q的建議的概率,也與Importance Sampling中的q(x)有同樣的作用。狀態轉換概率T(x→x')等於x' 被選中的概率乘上x' 被接受的概率,這和Importance Sampling同樣是一致的。因此,找合適的T變成找合適的q,而g可由q和希望的概率分佈f決定。
把上面兩個等式代入Detailed Balance的條件
並整理,得到
結果是,T消失了,而我們可以自由地選擇q(x)或g(x),只要保證上面的式子成立就行。
上式如果分子大於或等於分母,則等號右邊≥1,此時
那麼從當前狀態x轉換至q(x→x' )建議的狀態x' 應該被接受,因爲f(x' )也在上式的分子裏,它的值很可能處於f(x)之上的高處,而我們以前說過,在概率密度高的地方最好也更密集地採集樣本。由於接受概率不能大於1,我們取g(x→x' )=1。
如果分子小於分母,則f(x' )很可能但不肯定處於f(x )之下的低處。我們希望低處的樣本少於高處的樣本,但我們不能完全拒絕x' ,而是以一個概率接受x' 。我們取分母部分g(x' →x)=1,則接受x' 的概率
這時Detailed Balance仍然成立,同時狀態轉換得最快(請你想想爲什麼)。
歸納一下上面的兩種情況,Metropolis-Hastings算法使用如下的x→x' 的接受概率:
這裏需要問一個問題,在馬爾科夫鏈上跑Importance Sampling算法與常規的Importance Sampling有什麼不同或者說改進嗎?畢竟,MCMC也沒有告訴我們如何選擇最關鍵的q(x)。
它們之間重要的差別在於它們的g(x),當然q(x)也有差別,但這個差別比較隱祕。
如果我們爲MCMC選q(x)爲均勻分佈,就如同在一般的Rejection Sampling裏那樣,那麼,
因爲
如果q(x)選爲高斯分佈,注意,它與在一般的Importance Sampling裏使用的均值爲0的高斯分佈有所不同,它是以當前狀態爲均值(即中心值),以方差作爲超參數的非標準高斯分佈。此時,由於高斯分佈也具有對稱性,
所以,
總的來說,當q(x)具有對稱性時,
這是Metropolis-Hastings算法的核心結果。
可見,新的樣本被接受的概率取決於它與當前樣本點的相對高度,即f(x' )與f(x)之比,比較的基準是f(x)。
而在一般的Importance Sampling中,g(x' )= f(x' )/q(x' ) ,比較的基準是q(x' ),且與當前樣本點沒有關係,對每個新樣本點都是獨立地進行接受與否的判斷。
顯然,從比較的基準角度看,如果q(x)選爲高斯分佈,則多數情況下x→x' 跳的不太遠,MCMC的效率高於一般的Importance Sampling。同時,x→x' 也有一定的可能跳得較遠,即仍然有可能遍歷整個狀態空間,不至於總是在某些相鄰狀態之間徘徊,有助於提高採樣效率。而且,MCMC的最大的好處是,我們不必知道f(x)具體是什麼,而只要知道兩個樣本點之間的相對高度就可以決定是否接受新的樣本點。
MCMC的問題是,它必須從初始狀態運行一段時間後才能進入穩態,進入穩態後才能開始採樣。這段時間叫mixing time。我們無法知道MCMC系統什麼時候進入了穩態。雖然有一些跡象可作爲提示,但獲得這些跡象也並非簡單明瞭,而且也不能完全確定。
MCMC的另一個問題是,即使進入穩態,相鄰的採樣樣本之間很可能是有關聯的,而我們希望採集的樣本都是i.i.d.的。解決的方法是,每間隔多次(比如1000次)採樣再取一個樣本,或者同時跑多個(比如100個)獨立的馬爾科夫鏈,在它們上面輪流採樣。
無論用什麼解決辦法,這兩個問題都會影響MCMC的採樣效率和準確性。
總結一下采樣,我們走了"均勻分佈的採樣→高斯分佈的採樣→任意分佈的採樣"這樣一條路。
2.5 Bayesian Inference
現在,我們把MCMC用於Bayesian Inference,以獲得分佈參數的後驗概率。
根據MCMC方法,我們先用先驗概率P()以current爲中心值在其附近產生一個新的參數new。P()相當於MCMC裏的proposal分佈。正像以前那樣,我們一般選P()爲對稱的分佈,而且一般用高斯分佈。它的均值是當前參數current,方差則是一個超參數。方差的選擇對最後結果的誤差和MCMC算法的收斂速度有很大的影響,不過不是我們在這裏要討論的話題。
根據Metropolis-Hastings算法,這個新的參數是否被接受取決於目標分佈(此處即後驗概率)在new和current時的比例:
結果就是在new和current下的似然值之比(對數似然值之差)。如果這個比值大於等於1(對數似然值之差大於等於0),那麼new就被接受;如果小於1,則以這個比值爲概率接受new,未被接受時new = current。接着使new成爲新的current。
以new作爲新的current,不斷重複上述過程足夠多次,最後當MCMC進入穩態時,我們可以開始爲採樣。因爲我們把節點狀態概率設定爲後驗概率P(|D),所以在鏈上採集的樣本符合這個概率。統計這些樣本的empirical estimate就可以算出近似的後驗概率。如果運行的時間足夠長,MCMC也可以獲得任意精度的後驗概率。
但是,正如前面說過,採樣法的計算時間比較長,尤其是當數據集很大或者要近似的模型比較複雜時(模型複雜時後驗概率的狀態空間會很大,遍歷需更長時間)。下一章介紹的優化法,可以求得概率分佈(或其參數)的近似值,以精度換取時間。