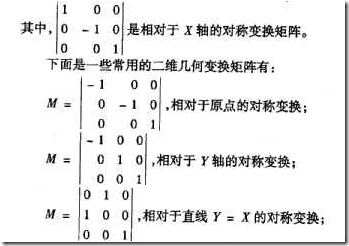
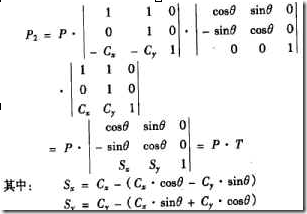轉載:http://www.cnblogs.com/Clingingboy/archive/2010/10/17/1853559.html
2.3.3 基本二維變換
基本二維變換有比例變換(Scaling)、旋轉變換(Rotating)、錯切變換(Shearing)和平移變換(Translating)。
1)比例變換
比例變換就是將平面上任意一點的橫座標放大或縮小S11倍,縱座標放大或縮小S22倍,即
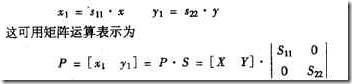
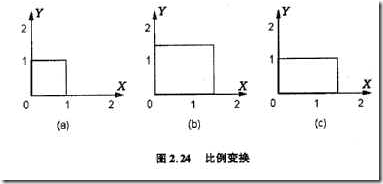
其中S稱爲比例變換矩陣。圖2.24是比例變換的幾個例子。圖中(b)是S11=S22的情況,(C)是S11≠S21的情況
2)旋轉變換
旋轉變換就是將平面上任意一點繞原點旋轉θ角,一般規定逆時針方向爲正,順時針方向爲負。從圖2.25可推出變換公式:

3)錯切變換
在旋轉變換矩陣中,非對角線元素有何幾何意義?觀察圖2.26中的例子。變換矩陣中元素S21起作把圖形沿X方向“錯切”的作用,Y值越小,錯切量越小。S12則有將圖形向Y方向“錯切”的作用,同樣其作用的大小與X值成正比。

4)平移變換
平移交換指的是將平面上任意一點沿X方向移動C。,沿Y方向移動ty(圖2.27),其變換公式爲
由上式可見,平移交換不能直接用2X2矩陣來表示。下述齊次座標變換矩陣則可解決這個問題。
注意:這句話關鍵(疑問點在於爲什麼二位轉換需要3x3的矩陣)
2.3.4 齊次座標
如把平面上的點P=[Xy]放到空間去表示爲[X Y H],使得x= X/H, y=Y/H 則稱[X Y H」是點 P的齊次座標。如規定齊次座標的第三個分量H必須是 1,則稱爲規範齊次座標。P=[xy」的規範齊次座標是[x y 1]。顯然,二維空間中描述的點與齊次座標空間描述的點是一對多的關係。使用齊次座標之後,平移交換可用矩陣乘法表示如下:
注意:現在可以看到平移的時候x1=x*1+x*0+x*tx,y1=y*0+y*1+y*ty即等於相加的做法,現在所有的轉換都可以使用矩陣乘法了
2.3.5 複合變換
實際問題中常遇到的是較爲複雜的變換,但這些均可通過一系列的基本變換複合而成。下面舉例說明。
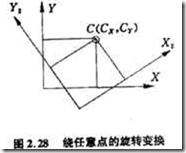
例1 繞任意點C=[Cx Cy]的旋轉變換。圖2.28總的變換可通過三個基本變換複合而成。先進行平移交換,平移量爲-Cx和-Cy,然後繞原點旋轉θ角,最後再進行平移量爲Cx和Cy的平移變換。因此,任一點P經過逐次變換後的齊次座標爲
變換矩陣稱爲複合變換矩陣。
例 2相對於任意點 C=[Cx Cy]的比例變換
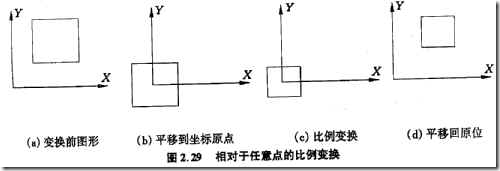
與例1其複合變換陣三個變換複合而成。即爲
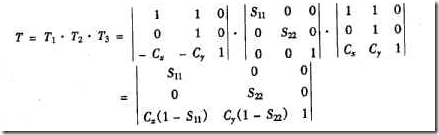
由上述計算過程知,一個簡單比例變換需要有三個計算步驟。對第一次平移,可看成是將變換物移動到座標系的原點,第二次平移則可看成將變換物移回原位。
例3 相對於直線 ax+by+c=0 進行對稱變換
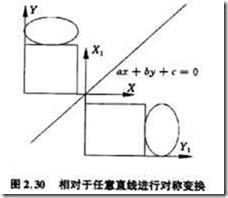
此例可由五個基本變換複合而成,複合變換矩陣可按下式進行計算