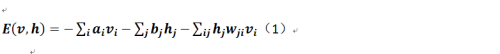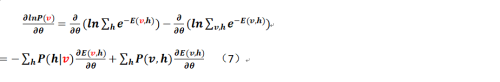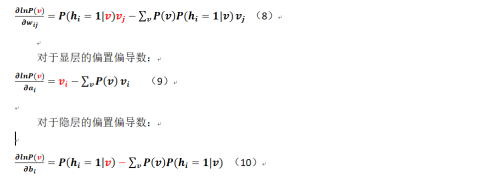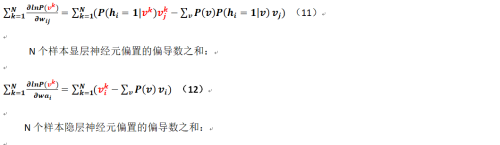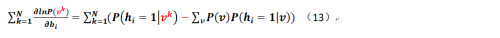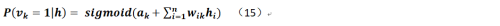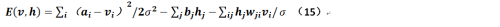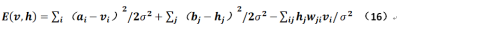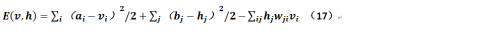前言
近一段時間以來筆者一直在查找關於受限玻爾茲曼機(Restricted Boltzmann Machine,下簡稱RBM)的相關資料,其實CSDN上的相關帖子已經其二值分佈的情況介紹的比較到位,而且在《機器學習》(於劍著)也以較短的篇幅描述了此類神經網絡的相關情況,但不知爲什麼此書的符號有點奇怪(在推導中涉及到顯層和隱層的偏置不是用很明顯的方式來表達的),而且似乎只推導到相關邊緣分佈,感覺讓人意猶未盡。
但是關於RBM的非二值情況(主要是實數,其模型源於高斯分佈)在網絡上總是無法查找到,幸而最近我在一個帖子中看到了相關內容,但沒有任何推導過程,只有結論。文中說這是Hinton教授一篇論文中所提到的,但我也沒有找到此論文的內容,不過根據最終的結論我給出了一個可能的推導,僅以本文記錄之。
不過在展開相關推導之前,還是想將RBM的相關基礎內容介紹一二,主要包括基於二值邏輯的RBM以作爲預備知識和必要的鋪墊。
另外,多說句閒話,這個RBM到底有什麼作用?其實它是一種無監督的訓練模型,一般可以作爲編碼壓縮(你可以認爲這是一種PCA方法)或作爲其它有監督訓練的預熱模型,以免在網絡初始訓練階段,各個需求的參數初值不靠譜而造成訓練時間過長。
相關定義和符號
能量
所謂RBM,就我個人理解而言,其實就是建立在玻爾茲曼能量分佈概率模型上的一個隨機系統,而RBM的網絡結構我也不費力解釋,這在各類文檔中有大量的闡述,總體而言它是一個含有m個顯層節點和n個隱層節點的網絡,而顯層和隱層之間是全連接的,但顯層和隱層內部的各個節點之間無任何聯繫,所以它也是一個二部圖。
對於受限玻爾茲曼的能量的定義如下:
這個公式其實不用過多解釋,其中v和h分別表示顯層和隱層,而a和b分別表示顯層和隱層的偏置,w(有兩個下標)則表示顯層節點和隱層節點之間連接的權重,很明顯它是一個m*n的矩陣。那麼在機器學習的範疇中是如何描述玻爾茲曼分佈的?
即其實Z是一個所謂的歸一化因子,它的結果就是整個網絡的能量之和(就是全部樣本的Power!因爲有隱層的存在,所以這個值其實好難求,這就是爲什麼需要使用GIBBS抽樣或對比散度抽樣來逼近這個)。
另外,爲了下面推導方便引入一個記號:
二值受限玻爾茲曼機的簡單推導
極大似然
我們討論的是非二值情況的RBM推導過程,但是爲了統一起見先推導下二值分佈的RBM。
任何機器學習問題,我們可能都會導向一個對目標函數最優值的求解問題,這個RBM也沒有任何例外,這目標函數爲一個以對數形式表達的似然函數:
但我們在後面可以看到,對於RBM而言其邊緣分佈及條件分佈都是極難獲得的!上式中表示每個樣本。
下面給出基於單個樣本v(被標識爲紅色,而黑色的v則表示所有樣本,下同)的似然公式:
爲了推導方便,現僅針對單個樣本的似然函數進行推導,多個樣本只是最終的一個樣本之和。
參數求解
那麼我們對公式(6)各個參數求偏導(按照慣例希臘字母θ表示各個待定的參數,即a、b和w),可以得到:
進而,對於各個參數的梯度而言,可以得到如下公式(其中過程中出現的各類繁瑣的推導就不再給出,可以參照CSDN的相關文檔,作者是皮果提,他給出的過程其實已經足夠詳細):
對於連接權重的偏導數:
那麼對於多個樣本而言相關公式又改是如何呢?現在假定我們有N個樣本(這個要和顯層、隱層的神經元數量進行區分),可得:
N個樣本連接權重的偏導數之和:
至此我們已經把N個樣本的相關各個參數的偏導形式求了出來!且慢,我們對於各個條件概率該如何求出(即對於公式7的第一部分該如何求解?第二部分該怎麼弄?那個只能求助於GIBBS或對比散度採樣),下面給出:
公式7的第一部分的直觀感覺是在顯層已知(這個是費話,因爲在初始情況下v就是樣本,當然已知)的情況下,怎麼得到隱層的條件分佈?這個推導是這樣的(筆者把參考的相關文檔倒過來進行分析,而且需注意這個是對一個樣本而言的,不是多個!):
那麼類似的,在隱層已知的情況下顯層相關神經元的值取1的條件概率是:
最後可將公式14、15分別帶入之前的相關推導結果就能得到完整的二值型受限玻爾茲曼機的公式。
經過筆者一段時間的思考,爲什麼網上介紹RBM基本上都是基於二值的(這個好像沒什麼用,因爲至少我要用256級灰度的圖像來學習,這個只能歸一化到(0,1)區間,難道要把神經元數量再乘以256,那麼對於MINST庫來說豈不是顯層的神經元有28*28*256個)?可能是此類網絡最後的推導結果正好可以使用sigmoid來表示吧?還是由於二值的邏輯非常簡單?但其實本文中的證明過程已經省略了很多,比如公式14中第4行是怎麼來的?就是把它們再用能量的方式表示出來,將除法運算轉化爲指數的減法運算而已(減去公共項)。
受限玻爾茲曼機的推導過程其實已經最夠複雜,但還好只是繁瑣而並不困難,關鍵點在於貝葉斯公式的使用,但對於連續型而言該如何處理?
非二值受限玻爾茲曼機的推導
上文提到,Hinton曾經在他的文章中給出過非二值的受限玻爾茲曼的條件概率公式(假定來自於均值爲μ,方差爲σ的高斯分佈),在給出這個公式推導之前,先重新定義下能量:
上述公式是令顯層的神經元是實值,而隱層神經元取值仍在{0,1}兩個離散值之間,根據相關對稱性,可以想見如果顯層和隱層均爲實值變量的話,則公式15應爲:
對於公式15和公式16應注意其符號的變化。但Hinton又在他的課程中指出,如果存在方差則造成訓練的失敗,那麼我們可以令方差σ=1,那麼公式16就變成:
以下我們就在這個基礎上推導相關條件概率公式。這裏需要強調的是其實推導本身沒有什麼複雜的,只不過使用了點積分知識,而且需記住在多元函數積分中,如果需要消除哪個變量那麼就應該對其進行積分,類似地對於離散情況也是如此,只不過把積分符號改成了求和符號而已;另外,通過下面的證明來看,消除一個變量總比消除多個變量來的方便些,公式看上去也簡單明瞭不少,否則按照貝葉斯公式的標準表達,則我們要進行多重積分以求得相關邊緣分佈。
由上節的基於二值受限玻爾茲曼機公式14啓發得:
至此我們得到了顯層對隱層的條件概率,而由其對稱性可知隱層對顯層的條件概率爲:
最終,對於非二值受限玻爾茲曼機的推導完成,請各位指正。至於算法流程和如何利用對比散度來進行抽樣,則這部分其實和二值受限玻爾茲曼機無甚區別,只不過對於後者而言是利用平均抽取,而前者採用正態分佈抽取而已。