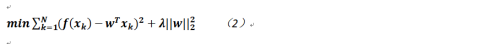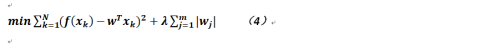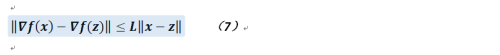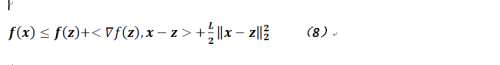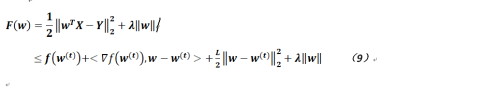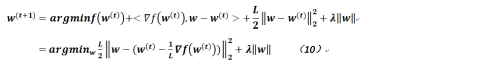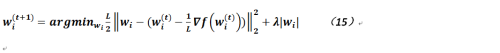在之前的文章中,筆者給出了關於最小二乘法相關公式的整體推導過程,最小二乘法本身除了可以利用數據進行相關參數的擬合(主要是係數和偏置),而且作爲分類問題中最爲簡單的模型也有着重要作用,我們也可以將其稱作最爲簡單的線性迴歸模型(以後需要涉及到支持向量機的問題,即Support Vector Machine這個其實也是一種線性迴歸模型,但在線性不可分的情況下,需要利用核函數對其進行相關處理),後面可能還會涉及到基於對數模型(多分類)的線性迴歸問題(這個叫法有點奇怪,既然是線性迴歸怎麼還和對數發生關係),這主要包括Softmax Regression和logistic Regression,但它們不是本文的討論範圍。
問題由來
筆者認爲,對於解決同樣問題,任何新方法提出的初衷可能都是由於原方法或技術無法解決或不能完美解決,所以本文所要重點討論的是關於一般線性迴歸模型在某些場合可能存在的問題,其實問題主要是由於樣本存在一定的相關性(就是樣本抽樣方法存在問題或樣本空間本身太小,這個問題其實在很多場合都存在,另外一種方法擴充樣本的方法是對其進行一定變型,這種方法可以在討論前饋神經網絡的時候涉及),其結果就會導致過擬合(Overfitting),在數學上的表現就是樣本矩陣及其樣本矩陣轉置的乘積是奇異的,即矩陣不可逆,這樣我們就無法利用推導出的公式進行計算了,爲了描述方便,現再次列出原公式,如下:
按照之前文章的約定,X就是一個n*m的矩陣,其中n就是樣本數量,而m是向量的維度,爲了討論方便,上式省略了偏置b。
這是一個Close Form,就是閉式解(所謂閉式解的含義就是我們可以公式直接獲得結果,但如果不是則可能需要藉助迭代的方法求解,比如牛頓法等)。
嶺迴歸
嶺迴歸(Ridge Regression)的提出就是爲了部分解決公式(1)中可能出現的矩陣不可逆的情況而提出的,否則會出現Leo Breiman所提出的羅生門現象,而造成解的不唯一性。在下面的論述中,我們仍然省略偏置,這個其實只要對樣本稍加處理即可,所以我們現在聚焦向量x的係數w。
其實如何解決這個問題,是比較簡單的。首先還是將線性迴歸的目標公式再列出:
其N是樣本的數量,而λ(大於等於0)被稱作正則化係數,用來控制收縮程度,它的值越小收縮程度越大,顯然當其爲0時則退化成原線性迴歸問題。
通過上述的處理,公式1就會變成如下的形式:
其中I是n*n的單位矩陣,故即便樣本及其轉置乘積不是滿秩的,加入後面的部分也能構成非奇異矩陣。
順便提一句,一般而言公式2本身是可導的,所以其求解是比較容易的,但下面討論的Lasso迴歸則不然,讀者需要注意其推導的不同(這個就比嶺迴歸要複雜一些,要使用一些看上去比較詭異的方法)。
Lasso迴歸
對於嶺迴歸而言,在公式2中我們可以看到和原始迴歸方法相比,多出的一項爲係數平方和,但這個計算複雜度略微有點高,如果我們只關心那些非零的係數則完全可以用一範數來替代二範數,就能達到幾乎同樣的效果,不過帶來的代價就是公式不可導;Lasso迴歸的目標公式如下:
其中m是向量的維度。
因爲它是一範數,故係數有更多的機會爲0(對應二範數而言),進而有可能得到更加稀疏的解。
現將公式4改寫成矩陣形式:
前面已經提到過了,與原始的線性迴歸及嶺迴歸不同的是,求解上式的難點在於一範數在零點不可導(絕對值的原因),所以它不像前兩者,沒有閉合解,而需要使用FIST(Fast Iterative Shrinkage Thresholding)方法,這種方法可以用於求解形如下式的目標函數:
其中g(x)爲連續的凸函數,可以不光滑,而f(x)則爲光滑函數,其導數應滿足利普希茨連續(Lipschitz Continuity),這個連續性比一般的一致連續性要求更強,即存在常數L(大於零),滿足對於定義域D上的任意兩個不同的實數x和z(其實可以擴充到其它符合要求的空間中,不一定非要是實數空間,不過度娘是這麼解釋的)都有:
上式給人直觀的感受就是把函數的變化收縮在一定範圍內,對於滿足條件最小的L而言,則稱其爲利普希茨常數,如果L < 1則f被稱作收縮映射。
νf(x)爲f(x)的梯度;根據相關文檔可以得到如下公式:
需要說明的一點是在上面的公式中,< ,>是內積符號,而且這個公式的右邊部分有點類似泰勒展開式(函數f(x)在點z的展開)。
現令,而令
,然後將f(w)在
處展開(這裏t表示w迭代了t次),由公式8可得如下公式:
通過上面的變形來看FIST方法最小化的並不是原函數,而是其一個上界函數(因爲L是大於零的),但經過變形的公式其實仍然無法求其導數,那麼可以去掉公式9的相關常數部分再添加一些常數(因爲在下面的公式中,我們使用了argmax/argmin函數,對於這個函數而言,加入或去除一些常數項是不影響最終得到的結果的,這點需要注意,否則無法理解其精髓)。經過處理的公式變爲如下形式:
最後的話
至於如何去迭代求解參數,感興趣的讀者可以在網上搜索,算法本身不是太複雜,最終參數w達到收斂即可;但這裏可能需要解釋的是公式11-13的含義,其實就我的理解而言由於目標函數不可導,我們通過一些處理使得它能達到要求,不是太嚴謹的話,你也可以這麼理解,即公式10可以按不同的維度寫作如下形式:
如果對上式求導也是無法進行的,那麼可以分別在大於0或小於0時進行求導並令其爲0,那麼實際得到的就是公式12,其中: