正文
第一節 問題的提出及解決方法
所謂最短路徑問題,可以說有兩種情況來描述。
描述一:在圖論中,指的是尋找圖中兩個節點之間的最短距離。如下圖
![]()
第一節 問題的提出及解決方法
所謂最短路徑問題,可以說有兩種情況來描述。
描述一:在圖論中,指的是尋找圖中兩個節點之間的最短距離。如下圖
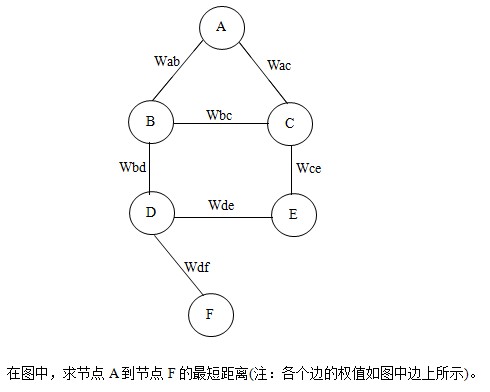
描述二:在現實生活中,指的是找到從一個地方到另一個地方的最近距離。如下圖
![]()

上述兩種情況的本質是一樣的,即求一個點到另一個點的最短路徑。好了,問題已經提出來了,那怎麼解決呢?解決該問題的方法還是比較多的,不過由於各個路徑算法所對應的問題條件不同,我們可根據不同的情況,選擇不同的路徑算法。
本文將介紹三種最短路徑算法,分別是:戴克斯特拉算法(Dijkstra algorithm),弗洛伊德算法(Floyd algorithm)以及A*搜索算法。
第二節 戴克斯特拉算法(Dijkstra algorithm)
該算法解決的是有向圖中單個源點到其他頂點的最短路徑問題。
戴克斯特拉算法的實現過程如下:
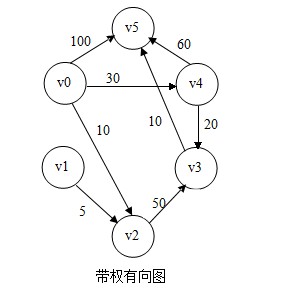
第一步:用帶權的矩陣WeiArcs來表示帶權有向圖,如果圖中的兩個頂點vi和vj是連通的,則用WeiArcs[i][j]表示這兩個頂點所形成邊的權值;如果vi和vj不連通,即<vi,vj>這條邊不存在,那麼將WeiArcs[i][j]置爲∞。
第二步:設S爲已求得的從某一頂點v始發的最短路徑的終點的集合,且S的初始狀態爲空,初始化時,將始發頂點置於S集合中。那麼從v出發到圖中其餘各個頂點vi可能達到的最短路徑長度的初值爲D[i]。
第三步:選擇一頂點vj,使得vj就是當前求得的一條從頂點v出發的最短路徑的終點。此時令S = S ∪ {vj}。
第四步:修改從v出發到集合V-S(V爲圖頂點的集合)中任一頂點vk可達的最短路徑長度。如果D[j]+WeiArcs[j][k] < D[K],則D[k] = D[j] + WeiArcs[j][k]。
第五步:重複操作第三步、第四步共N-1次,由此就能求得從v出發到圖中其餘各個頂點的最短路徑。
好了,實現過程就是這樣。不過光有文字描述不行,要更直白的表達這個過程,我認爲用圖像表述是一個很好的選擇。如下圖所示
![]()
![]()
![]()
本文將介紹三種最短路徑算法,分別是:戴克斯特拉算法(Dijkstra algorithm),弗洛伊德算法(Floyd algorithm)以及A*搜索算法。
第二節 戴克斯特拉算法(Dijkstra algorithm)
該算法解決的是有向圖中單個源點到其他頂點的最短路徑問題。
戴克斯特拉算法的實現過程如下:
第一步:用帶權的矩陣WeiArcs來表示帶權有向圖,如果圖中的兩個頂點vi和vj是連通的,則用WeiArcs[i][j]表示這兩個頂點所形成邊的權值;如果vi和vj不連通,即<vi,vj>這條邊不存在,那麼將WeiArcs[i][j]置爲∞。
第二步:設S爲已求得的從某一頂點v始發的最短路徑的終點的集合,且S的初始狀態爲空,初始化時,將始發頂點置於S集合中。那麼從v出發到圖中其餘各個頂點vi可能達到的最短路徑長度的初值爲D[i]。
第三步:選擇一頂點vj,使得vj就是當前求得的一條從頂點v出發的最短路徑的終點。此時令S = S ∪ {vj}。
第四步:修改從v出發到集合V-S(V爲圖頂點的集合)中任一頂點vk可達的最短路徑長度。如果D[j]+WeiArcs[j][k] < D[K],則D[k] = D[j] + WeiArcs[j][k]。
第五步:重複操作第三步、第四步共N-1次,由此就能求得從v出發到圖中其餘各個頂點的最短路徑。
好了,實現過程就是這樣。不過光有文字描述不行,要更直白的表達這個過程,我認爲用圖像表述是一個很好的選擇。如下圖所示

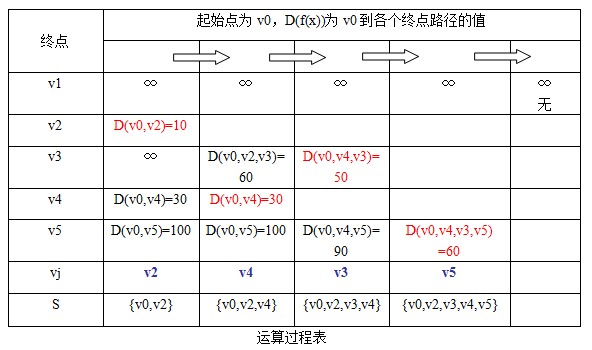
從運算過程表中,我們可知v0到其餘個點的最短路徑,如下圖
![]()

上述過程描述的戴克斯特拉算法的代碼如下:
第三節 弗洛伊德算法(Floyd algorithm)
該算法解決的是有向帶權圖中兩頂點之間最短路徑的問題。
弗洛伊德算法的設計過程如下:
用帶權的矩陣WeiArcs來表示帶權有向圖,如果圖中的兩個頂點vi和vj是連通的,則用WeiArcs[i][j]表示這兩個頂點所形成邊的權值;如果vi和vj不連通,即<vi,vj>這條邊不存在,那麼將WeiArcs[i][j]置爲∞。
要求:求節點vi到節點vj的最短路徑。
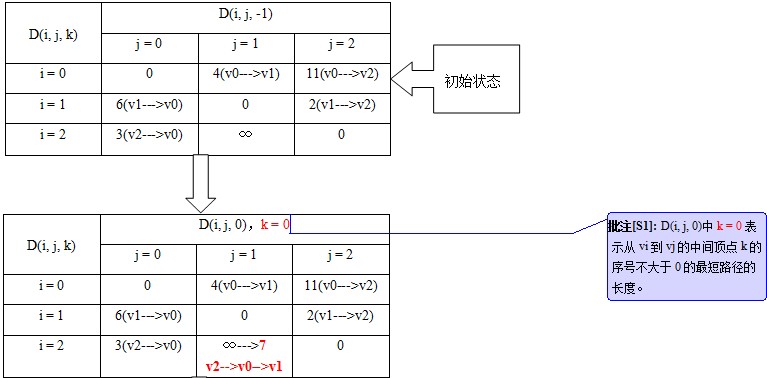
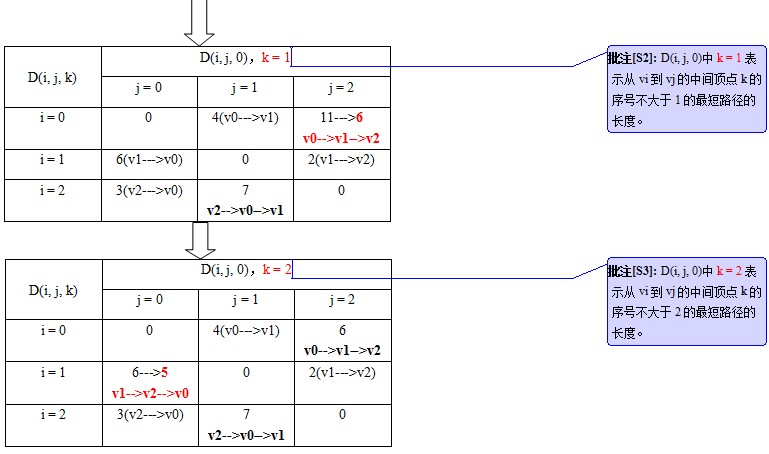
設D(i,j,k)爲從節點vi到節點vj的以vk(vk∈(0,1,...k))節點爲中間節點的最短路徑的長度。例如:從vi到vj這條路徑上經過節點vm和節點vk,那麼可表示爲:vi-->vm-->vk-->vj。
那麼,就有:1.若最短路徑經過節點vk,則D(i,j,k) = D(i,k,k-1) + D(k,j,k-1);
2.若最短路徑不經過節點vk,則D(i,j,k) = D(i,j,k-1)。
所以,求的vi到vj的最短路徑可表示爲:
![]()
int ShortPath(MGraph G,int v0,PathMatrix &P,ShortPathTable &D) { //用戴克斯特拉算法求有向圖G中v0頂點到其餘頂點v的最短路徑P[v]及帶權長度D[v]。 //若P[v][w]爲TRUE,則w是從v0到v當前求得最短路徑上的頂點。 //final[v]爲TRUE當且僅當v∈S,即已經求得從v0到v的最短路徑。 for(v = 0;v < G.vexmun;v++) { final[v] = FALSE; D[v] = G.WeiArcs[v0][v]; for(w = 0;w < G.vexnum;w++) P[v][w] = FALSE; //設空路徑 if(D[v] < INFINITY) { p[v][v0] = TRUE; p[v][v] = TRUE; } } D[v0] = 0;final[v0] = TRUE; //初始化,v0頂點屬於S集合 //開始主循環,每次求得v0到某個頂點v的最短路徑,並將v加到S集合中 for(i = 1; i < G.vexnum; i++) //其餘G.vexnum - 1個頂點 { min = INFINITY; //當前所知離v0點的最近距離 for(w = 0;w < G.vexnum; i++) { if(!final[w]) //w頂點在V - S中 { if(D[w] < min) //w頂點離v0更近 { v = w; min = D[w]; } } } final[v] = TRUE; //離v0頂點最近的v加入到S中 for(w = 0;w < G.vexnum;w++) //更新當前最算路徑及距離 { if(!final[w] && (min + G.WeiArcs < D[w])) { D[w] = min + G.WeiArcs[v][w]; //p[w] = P[v] + P[w]; P[w] = P[v]; P[w][w] = TRUE; } } } return 0; }ok,Dijkstra algorithm介紹完了。第三節 弗洛伊德算法(Floyd algorithm)
該算法解決的是有向帶權圖中兩頂點之間最短路徑的問題。
弗洛伊德算法的設計過程如下:
用帶權的矩陣WeiArcs來表示帶權有向圖,如果圖中的兩個頂點vi和vj是連通的,則用WeiArcs[i][j]表示這兩個頂點所形成邊的權值;如果vi和vj不連通,即<vi,vj>這條邊不存在,那麼將WeiArcs[i][j]置爲∞。
要求:求節點vi到節點vj的最短路徑。
設D(i,j,k)爲從節點vi到節點vj的以vk(vk∈(0,1,...k))節點爲中間節點的最短路徑的長度。例如:從vi到vj這條路徑上經過節點vm和節點vk,那麼可表示爲:vi-->vm-->vk-->vj。
那麼,就有:1.若最短路徑經過節點vk,則D(i,j,k) = D(i,k,k-1) + D(k,j,k-1);
2.若最短路徑不經過節點vk,則D(i,j,k) = D(i,j,k-1)。
所以,求的vi到vj的最短路徑可表示爲:
D(i,j,k) = min(D(i,k,k-1) + D(k,j,k-1), D(i,j,k-1))。
老辦法,圖示的過程如下: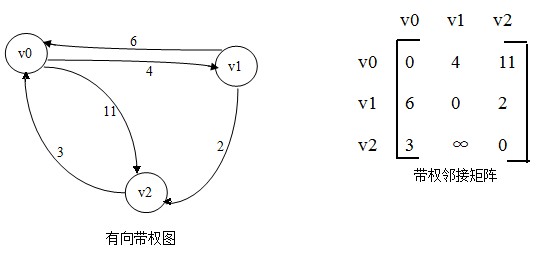
求解的過程見下圖:
![]()
![]()
上述過程描述的弗洛伊德算法的代碼如下:
第四節 A*搜索算法
A*搜索算法,俗稱A星算法。這是一種在圖平面上,有多個節點的路徑,求出最低通過成本的算法。常用於遊戲中的NPC的移動計算,或線上遊戲的BOT的移動計算上。該算法像Dijkstra算法一樣,可以找到一條最短路徑;也像BFS一樣,進行啓發式的搜索。
A*算法最核心的部分,就在於它的一個估值函數的設計上:f(n)=g(n)+h(n)。其中,g(n)表示從起始點到任一點n的實際距離,h(n)表示任意頂點n到目標頂點的估算距離,f(n)是每個可能試探點的估值。這個估值函數遵循以下特性:
int ShortPath(MGraph G,int v0,PathMatrix &P,ShortPathTable &D) { //用Floyd算法求有向圖中各對頂點v和w之間的最短路徑P[v][w]及其帶權長度D[v][w]。 //若p[v][w][u]爲TRUE,則u是從v到w當前求得的最短路徑上的頂點 for(v = 0;v < G.vexnum;v++) for(w = 0;w < G.vexnum;w++) { D[v][w] = G.arcs[v][w]; if(D[v][w] < INFINITY) //從v到w有直接路徑 { P[v][w][u] = TRUE; P[v][w][w] = TRUE; } } for(u = 0;u < G.vexnum;u++) for(v = 0;v < G.vexnum;v++) for(w = 0;w < G.vexnum;w++) { if(D[v][u] + D[u][w] < D[v][w]) //從v經u到w的一條更短路徑 D[v][w] = D[v][u] < D[u][w]; for(i = 0;i < G.vexnum;i++) P[v][w][i] = P[v][u][i] || P[u][w][i]; } return 0; }第四節 A*搜索算法
A*搜索算法,俗稱A星算法。這是一種在圖平面上,有多個節點的路徑,求出最低通過成本的算法。常用於遊戲中的NPC的移動計算,或線上遊戲的BOT的移動計算上。該算法像Dijkstra算法一樣,可以找到一條最短路徑;也像BFS一樣,進行啓發式的搜索。
A*算法最核心的部分,就在於它的一個估值函數的設計上:f(n)=g(n)+h(n)。其中,g(n)表示從起始點到任一點n的實際距離,h(n)表示任意頂點n到目標頂點的估算距離,f(n)是每個可能試探點的估值。這個估值函數遵循以下特性:
©著作權歸作者所有:來自51CTO博客作者SuperFengstark的原創作品,如需轉載,請註明出處,否則將追究法律責任
0
收藏





Ctrl+Enter 發佈
發佈
取消